已知函数 .
.
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明 在
在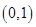 上是减函数;
上是减函数;
(本小题满分12分)在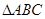 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若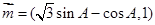 ,
,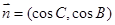 ,且
,且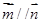 .
.
(1)求角B的大小;
(2)若 ,求b的取值范围.
,求b的取值范围.
(本小题满分10分)已知数列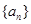 各项均为正,且
各项均为正,且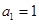 ,
,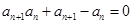
 .
.
(1)设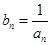 ,求证:数列
,求证:数列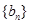 是等差数列;
是等差数列;
(2)求数列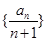 的前n项和
的前n项和 .
.
(本小题满分12分)设 ,
,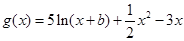 ,函数
,函数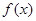 在
在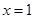 与
与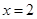 处取得极值.
处取得极值.
(1)求实数a,b的值;
(2)若 ,求证:当
,求证:当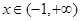 时,
时,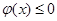 恒成立;
恒成立;
(3)证明:若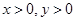 ,则
,则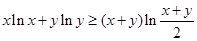 .
.
(本小题满分12分)已知点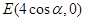 ,
,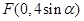
 为平面直角坐标系
为平面直角坐标系 中的点,点P为线段EF的中点,当
中的点,点P为线段EF的中点,当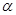 变化时,点P形成的轨迹
变化时,点P形成的轨迹 与x轴交于点A,B(A点在左侧),与y轴正半轴交于点C.
与x轴交于点A,B(A点在左侧),与y轴正半轴交于点C.
(1)求P点的轨迹 的方程;
的方程;
(2)设点M是轨迹 上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
①若D点坐标为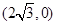 ,求线段CM的长;
,求线段CM的长;
②求证: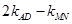 为定值.
为定值.
(本小题满分12分)在如图所示的几何体中, 与
与 都是边长为2的等比三角形且所在平面互相平行,四边形BCED为正方形,
都是边长为2的等比三角形且所在平面互相平行,四边形BCED为正方形, ,O,G分别是BC,DE的中点.
,O,G分别是BC,DE的中点.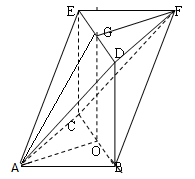
(1)证明:平面ADE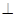 平面AOFG;
平面AOFG;
(2)求二面角D-AE-F的余弦值.