在平面直角坐标系中,O为坐标原点,已知点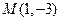 ,
,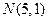 ,若点C满足
,若点C满足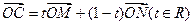 ,点C的轨迹与抛物线
,点C的轨迹与抛物线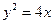 交于A、B两点.
交于A、B两点.
(I)求证: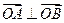 ;
;
(II)在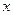 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点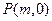 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
(本题满分16分,第(1)小题8分,第(2)小题8分)
己知双曲线的中心在原点,右顶点为
 (1,0),点
(1,0),点 、Q在双曲线的右支上,点
、Q在双曲线的右支上,点 (
(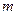 ,0)到直线
,0)到直线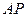 的距离为1.
的距离为1.
(1)若直线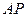 的斜率为
的斜率为 且有
且有 ,求实数
,求实数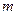 的取值范围;
的取值范围;
(2)当 时,
时,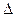
 的内心恰好是点
的内心恰好是点 ,求此双曲线的方程.
,求此双曲线的方程.
(本题满分16分,第(1)小题6分,第(2)小题10分)
如图,已知点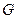 是边长为
是边长为 的正三角形
的正三角形 的中心,线段
的中心,线段 经过点
经过点 ,并绕点
,并绕点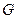 转动,分别交边
转动,分别交边 、
、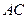 于点
于点 、
、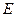 ;设
;设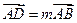 ,
,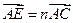 ,其中
,其中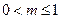 ,
,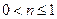 .
.
(1)求表达式 的值,并说明理由;
的值,并说明理由;
(2)求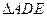 面积的最大和最小值,并指出相应的
面积的最大和最小值,并指出相应的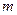 、
、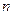 的值.
的值.
(本题满分14分,第(1)小题6分,第(2)小题8分)
设全集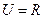 ,关于
,关于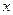 的不等式
的不等式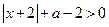 (
(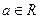 )的解集为
)的解集为 .
.
(1)分别求出当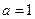 和
和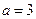 时的集合
时的集合 ;
;
(2)设集合 ,若
,若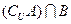 中有且只有三个元素,求实数
中有且只有三个元素,求实数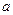 的取值范围.
的取值范围.
(本题满分12分,第(1)小题6分,第(2)小题6分)
如图,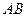 是圆柱体
是圆柱体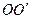 的一条母线,
的一条母线,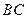 过底面圆的圆心
过底面圆的圆心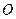 ,
, 是圆
是圆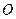 上不与点
上不与点 、
、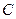 重合的任意一点,已知棱
重合的任意一点,已知棱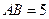 ,
,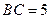 ,
,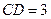 .
.
(1)求直线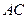 与平面
与平面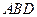 所成的角的大小;
所成的角的大小;
(2)将四面体 绕母线
绕母线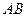 转动一周,求
转动一周,求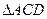 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
(本小题满分14分)
某工厂生产一种产品的成本费由三部分组成:
① 职工工资固定支出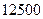 元;② 原材料费每件40元;
元;② 原材料费每件40元;
③ 电力与机器保养等费用为每件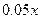 元,其中
元,其中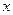 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费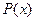 (元)表示成产品件数
(元)表示成产品件数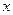 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量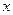 不超过
不超过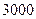 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价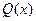 与产品件数
与产品件数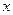 有如下关系:
有如下关系: ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)