如图，C为∠AOB的边OA上一点，OC＝6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．
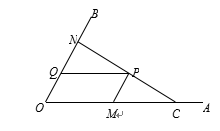
（1）若∠AOB＝60º，OM＝4，OQ＝1，求证：CN⊥OB．
（2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
①问：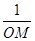
－
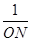的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．
②设菱形OMPQ的面积为S1，△NOC的面积为S2，求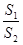
的取值范围．
已知二次函数y=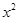
+bx+c的图象如图所示，它与x轴的一个交点的坐标为（－1，0），与y轴的交点坐标为（0，－3）．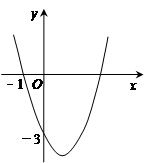
（1）求此二次函数的解析式；
（2）求此二次函数的图象与x轴的另一个交点的坐标；
（3）根据图象回答：当x取何值时，y＜0？
如图是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且AB = 26m，OE⊥CD于点E．水位正常时测得OE∶CD=5∶24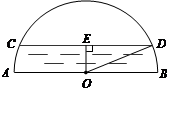
（1）求CD的长；
（2）现汛期来临，水面要以每小时4 m的速度上升，则经过多长时间桥洞会刚刚被灌满？
某商场销售一批名牌衬衣，平均每天可售出20件，每件衬衣盈利40元.为了扩大销售，
增加盈利，尽快减少库存，商场决定采取适当的降价措施.经调查发现，如果每件衬衣降价1元，商场平均
每天可多售出2件.
（1）若商场平均每天盈利1200元，每件衬衣应降价多少元？
（2）若要使商场平均每天的盈利最多，请你为商场设计降价方案.
如图，在△ABC中，∠C=90°, AD是∠BAC的平分线，O是AB上一点, 以OA为半径的⊙O经过点D。
（1）求证： BC是⊙O切线；
（2）若BD="5," DC="3," 求AC的长。
计算：是某几何体的平面展开图，求图中小圆的半径． 