如图，已知抛物线y=ax2+bx+c（经过原点）与x轴相交于N点，直线y=kx+4与坐标轴分别相交于A、D两点，与抛物线相交于B（1，m）和C（2，2）两点．
（1）求直线与抛物线的表达式；
（2）求证：C点是△AOD的外心；
（3）若（1）中的抛物线，在x轴上方的部分，有一动点P（x，y），设∠PON=α．当sinα为何值时，△PON的面积有最大值？
（4）若P点保持（3）中运动路线，是否存在△PON，使得其面积等于△OCN面积的
？若存在，求出动点P的位置；若不存在，请说出理由．
某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长69米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的而积最大？下面是两位学生争议的情境：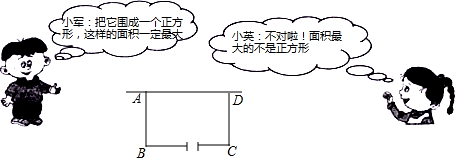
请根据上面的信息，解决问题：
（1）设AB=x米（x＞0），试用含x的代数式表示BC的长；
（2）请你判断谁的说法正确，为什么？
如图，在平面直角坐标系中，点A（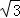
，1）、B（2，0）、O（0，0），反比例函数y=
图象经过点A．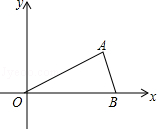
（1）求k的值；
（2）将△AOB绕点O逆时针旋转60°，得到△COD，其中点A与点C对应，试判断点D是否在该反比例函数的图象上？
在Rt△ACB和Rt△AEF中，∠ACB=∠AEF=90°，若点P是BF的中点，连接PC，PE．
特殊发现：如图1，若点E，F分别落在边AB，AC上，则结论：PC=PE成立（不要求证明）．
问题探究：把图1中的△AEF绕着点A顺时针旋转．
（1）如图2，若点E落在边CA的延长线上，则上述结论是否成立？若成立，请给予证明；若不成立，请说明理由；
（2）如图3，若点F落在边AB上，则上述结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；
（3）记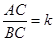
，当k为何值时，△CPE总是等边三角形？（请直接写出k的值，不必说明理由）
抛物线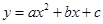
，若a，b，c满足b=a+c，则称抛物线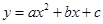为“恒定”抛物线．
（1）求证：“恒定”抛物线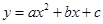必过x轴上的一个定点A；
（2）已知“恒定”抛物线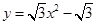
的顶点为P，与x轴另一个交点为B，是否存在以Q为顶点，与x轴另一个交点为C的“恒定”抛物线，使得以PA，CQ为边的四边形是平行四边形？若存在，求出抛物线解析式；若不存在，请说明理由．
某动车站在原有的普通售票窗口外新增了无人售票窗口，普通售票窗口从上午8点开放，而无人售票窗口从上午7点开放，某日从上午7点到10点，每个普通售票窗口售出的车票数
（张）与售票时间x（小时）的变化趋势如图1，每个无人售票窗口售出的车票数
（张）与售票时间x（小时）的变化趋势是以原点为顶点的抛物线的一部分，如图2，若该日截至上午9点，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同．
（1）求图2中所确定抛物线的解析式；
（2）若该日共开放5个无人售票窗口，截至上午10点，两种窗口共售出的车票数不少于900张，则至少需要开放多少个普通售票窗口？