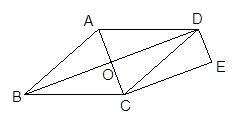如图,在平面直角坐标系中,点A(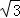 ,1)、B(2,0)、O(0,0),反比例函数y=
,1)、B(2,0)、O(0,0),反比例函数y= 图象经过点A.
图象经过点A.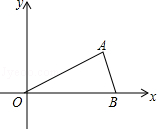
(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,试判断点D是否在该反比例函数的图象上?
世界上大部分国家都使用摄氏(℃)温度,但美、英等国的天气预报仍然使用华氏(℉)温度,两种计量之间有如下对应:
| ℃ |
0 |
10 |
20 |
30 |
| ℉ |
32 |
50 |
68 |
86 |
(1)设摄氏温度为 (℃),华氏温度为
(℃),华氏温度为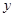 (℉),如果这两种计量之间的关系是一次函数,请求出该一次函数表达式.
(℉),如果这两种计量之间的关系是一次函数,请求出该一次函数表达式.
(2)求出华氏0度时摄氏是多少度.
(3)华氏温度的值与对应的摄氏温度的值有相等的可能吗?请说明理由.
某社区要在如图所示AB所在的直线上建一图书室E,并使图书室E到本社区两所学校C和D的距离相等(C、D所在位置如图所示),
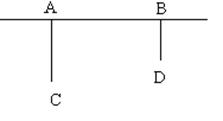
(1)请用圆规和直尺在图中作出点E;(不写作法,保留作图痕迹)
(2)求图书室E到点A的距离.
在平面直角坐标系中,点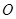 为原点,直线
为原点,直线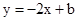 交x轴于点
交x轴于点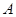 ,交
,交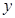 轴于点
轴于点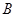 .若
.若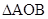 的面积为4,求
的面积为4,求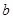 的值.
的值.
已知直线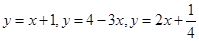 ,它们能交于同一点吗?为什么?
,它们能交于同一点吗?为什么?
如图,点O是菱形ABCD对角线的交点,过点C作BD的平行线CE,过点D作AC的平行线DE,CE与DE相交于点E,试说明四边形OCED是矩形.