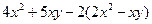如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出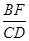 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)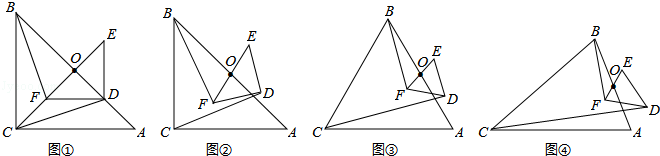
已知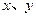 满足
满足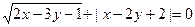 ,求
,求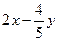 的平方根.
的平方根.
今年十月份,为方便民众出行,连江县成立了出租车公司,收费标准是:起步价5元,可乘坐3千米;3千米之后每千米加收1.8元.若某人乘坐了x千米,
(1)用代数式表示他应支付的费用;
(2)若他乘坐了13千米,应支付多少元?
为体现社会对老师的尊重,教师节这一天上午,出租车司机小王在东西向的公路上免费接送老师,如果规定向东为正,向西为负,出租车的行程如下(单位:千米) :+5,-4,+3,-10,+3,-9。
:+5,-4,+3,-10,+3,-9。
(1)最后一名老师送到目的时,小王距出租车出发点的距离是多少?
(2)若汽车耗油量为0.4升/千米,这天下午小王的汽车共耗油多少升?
先化简,再求值:
求代数式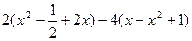 的值.其中
的值.其中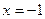
化简(每小 题5分,共10分)
题5分,共10分)
(1) 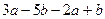 (2)
(2)