（来宾）某校有学生2000名，为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况，对学生开展了随机调查，丙将结果绘制成如下的统计图．
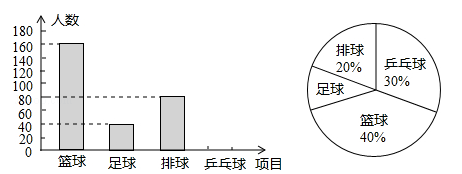
请根据以上信息，完成下列问题：
（1）本次调查的样本容量是 ；
（2）某位同学被抽中的概率是 ；
（3）据此估计全校最喜爱篮球运动的学生人数约有 名；
（4）将条形统计图补充完整．
我国是一个淡水资源严重缺乏的国家，有关数据显示，中国人均淡水资源占有量仅为美国人均淡水资源占有量的
，中、美两国人均淡水资源占有量之和为13800
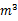，问中、美两国人均淡水资源占有量各为多少（单位：）？
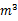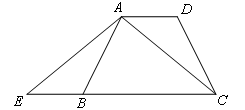
如图，在梯形ABCD中，已知AD∥BC，AB=CD，延长线段CB到E，使BE=AD，连接AE、AC.求证：△ABE≌△CDA；
若∠DAC=40°，求∠EAC的度数.
已知一抛物线经过
（0，0），
（1，1）两点，且解析式的二次项系数为
（
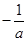
＞0）.当
时，求该抛物线的解析式，并用配方法求出该抛物线的顶点坐标；已知点
（0，1），若抛物线与射线
相交于点
，与
轴相交于点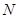
（异于原点），当在什么范围内取值时，
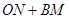的值为常数？当在什么范围内取值时，
的值为常数？若点
（
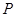，）在抛物线上，则称点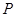为抛物线的不动点.将这条抛物线进行平移，使其只有一个不动点，此时抛物线的顶点是否在直线
上，请说明理由.
已知点P是直线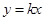
（
＞0，）上一定点，点A是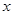
轴上一动点（不与原点重合），连结PA，过点P作PB⊥PA，交
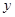轴于点B，探究线段PA与PB 的数量关系.如图（1），当PA⊥
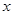轴时，观察图形发现线段PA与PB的数量关系是__________；当PA与
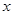轴不垂直时，在图（2）中画出图形，线段PA与PB 的数量关系是否与（Ⅰ）所得结果相同？写出你的猜想并加以证明；为何值时，线段PA=PB？此时∠POA的度数是多少，为什么？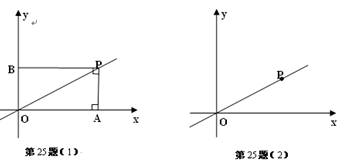
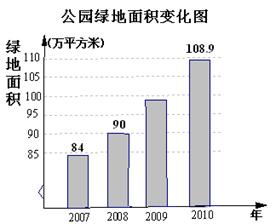
某新建公园的绿化给公园自身及周边的环境都带来了明显的改变，下面的条形图是这个新建公园近几年来绿地面积的变化图，请你根据图中所给的数据解答下列问题：求这个公园2008年底至2010年底这两年绿地面积的年平均增长率；
如果这个平均增长率保持不变，请你预测2011年底这个公园的绿地面积将达到多少万平方米？
