2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题: 
(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?
(本题5分,共10分) 解方程:
(1) ;(2)
;(2) .
.
某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为 () .
| A.x(x+1)=1035 |
| B.x(x-1)=1035×2 |
| C.x(x-1)=1035 |
| D.2x(x+1)=1035 |
(本题14分)在平面直角坐标系中,O为原点,四边形OABC的顶点A在 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥ 轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出 的取值范围.
的取值范围.
(本题12分)正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.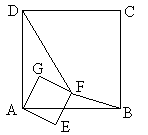
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
(本题12分)某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮.
(1)如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM:AN=8:9,问通道的宽是多少?
(2)为了建造花坛,要修改(1)中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛.如图3,在草坪RPCQ中,已知RE⊥PQ于点E,CF⊥PQ于点F,求花坛RECF的面积.