(1)【问题发现】小明遇到这样一个问题:
如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.
(1)小明发现,过点D作DF//AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系: ;
(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件
不变),试猜想AD与DE之间的数量关系,并证明你的结论.
(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,
请直接写出△ABC与△ADE的面积之比.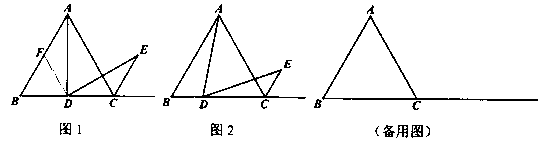
(满分8分)若关于 的一元二次方程
的一元二次方程 没有实数根,试化简:
没有实数根,试化简: .
.
解下列方程(每小题4分,满分8分):
(1)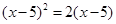
(2)
已知在四边形ABCD中,∠A="x," ∠C=y,(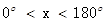 ,
, 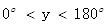 ).
).
(1)∠ABC + ∠ADC=(用含x、y的代数式表示) ;
(2)如图1,若x=y=90°,DE平分∠ADC ,BF平分与∠ABC相邻的外角,请写出DE 与 BF 的位置关系,并说明理由.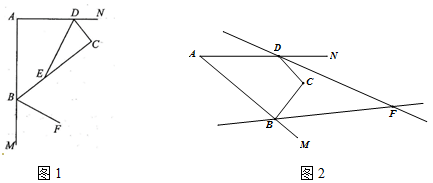
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x﹤y时,若x+y=140°,∠DFB=30°试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,
∠DFB不存在.
阅读下列材料解决问题:
将下图一个正方形和三个长方形拼成一个大长方形,观察这四个图形的面积与拼成的大长方形的面积之间的关系.
∵用间接法表示大长方形的面积为:x2+px+qx+pq,用直接法表示面积为:(x+p)(x+q)
∴x2+px+qx+pq=(x+p)(x+q)
∴我们得到了可以进行因式分解的公式:x2+(p+q )x+pq=(x+p)(x+q)
(1)运用公式将下列多项式分解因式:
①x2+6x+8②y2+7y-18
(2)如果二次三项式“a2+□ab+□b2”中的“□”只能填入有理数2、3、4(两个“□”内数字可以相同),并且填入后的二次三项式能进行因式分解,请你写出所有的二次三项式及因式分解的结果.
为支援灾区学生,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?