如图,在平行四边形ABCD中,AB=5,BC=12,对角线交于点O,∠BAD的平分线交BC于E、交BD于F,分别过顶点B、D作AE的垂线,垂足为G、H,连接OG、OH.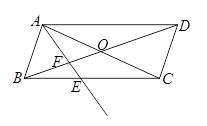
(1)补全图形;
(2)求证:OG=OH;
(3)若OG⊥OH,直接写出∠OAF的正切值.
作图题:如图,在Rt△ABC中,∠ACB=90度.利用尺规作图,把Rt△ABC分割成两个等腰三角形.
某中学为了筹备校庆活动,准备印制一批校庆纪念册。该纪念册分A、B两种,每册都需要10张8K大小的纸,其中A纪念册有4张彩色页和6张黑白页组成;B纪念册有6张彩色页和4张黑白页组成。印制这批纪念册的总费用由制版费和印制费两部分组成,制版费与印数无关,价格为:彩色页300元∕张,黑白页50元∕张;印制费与总印数的关系见下表。
总印数 (单位:千册) (单位:千册) |
 |
 |
| 彩色(单位:元∕张) |
2.2 |
2.0 |
| 黑白(单位:元∕张) |
0.7 |
0.5 |
印制这批纪念册的制版费为元。
若印制A、B两种纪念册各2千册,则共需多少费用?
如果该校共印制了A、B两种纪念册6千册,一共花费了75500元,则该校印制了A、B两种纪念册各多少册?
CD是经过∠BCA的顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=∠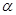 ,若直线CD经过∠BCA的内部,且E、F在射线C、D上,请解答下面的三个问题:
,若直线CD经过∠BCA的内部,且E、F在射线C、D上,请解答下面的三个问题:如图1,若∠BCA=
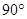 ,∠
,∠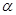 =
=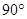 ,则∠BCE∠CAF;BECF(填“﹥”、“﹤”、“=”);并证明这两个结论。
,则∠BCE∠CAF;BECF(填“﹥”、“﹤”、“=”);并证明这两个结论。如图2,若∠BCA=
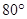 ,要使∠BCE与∠CAF有(1)中的结论,则∠
,要使∠BCE与∠CAF有(1)中的结论,则∠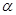 =;
=;如图2,若
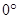 ﹤∠BCA﹤
﹤∠BCA﹤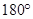 ,当∠
,当∠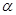 与∠BCA满足什么关系时,则(1)中的两个结论仍然成立。这个关系是。(只填结论,不用证明)
与∠BCA满足什么关系时,则(1)中的两个结论仍然成立。这个关系是。(只填结论,不用证明)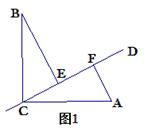

有一枚均匀的正四面体,四个面上分别标有数字l,2,3,4,小红随机地抛掷一次,把着地一面的数字记为x;另有三张背面完全相同,正面上分别写有数字一2,一l,1的卡片,小亮将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后他们计算出 的值.
的值.用树状图或列表法表示出S的所有可能情况;
分别求出当S=0和S<2时的概率.
如图,在所给的网格图(每小格边长均为1的正方形)中,完成下列各题:将△ABC向右平移4个单位得到△A1B1C1;
以直线
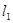 为对称轴作△ABC的轴对称图形△
为对称轴作△ABC的轴对称图形△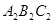 ;
;△
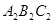 可以看作是由△A1B1C1先向左平移4个单位,再以直线
可以看作是由△A1B1C1先向左平移4个单位,再以直线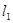 为对称轴作轴对称变换得到的。除此以外,△
为对称轴作轴对称变换得到的。除此以外,△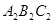 还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。
还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。