(本小题满分12分)如图(1),在直角梯形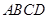 中,
中,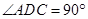 ,
,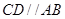 ,
,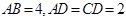 .将
.将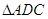 沿
沿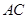 折起,使平面
折起,使平面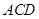
 平面
平面 ,得到几何体
,得到几何体 ,如图(2)所示.
,如图(2)所示.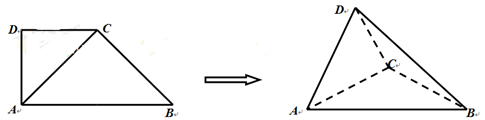
(1)求证: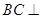 平面
平面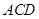 ;
;
(2)求二面角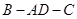 的正切值.
的正切值.
已知圆C的方程
(1)若点 在圆C的内部,求m的取值范围;
在圆C的内部,求m的取值范围;
(2)若当 时
时
①设 为圆C上的一个动点,求
为圆C上的一个动点,求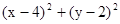 的最值;.
的最值;.
②问是否存在斜率是1的直线l,使l被圆C截得的弦AB,以AB为直径的圆经过原点,若存在,写出直线l的方程;若不存在,说明理由.
在长方体 中,
中,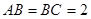 ,过
,过 ,
,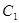 ,
, 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,这个几何体的体积为
,这个几何体的体积为 。
。
(1)证明:直线 ∥平面
∥平面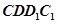 ;
;
(2)求棱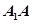 的长;
的长;
(3)在线段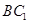 上是否存在点
上是否存在点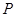 ,使直线
,使直线 与
与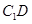 垂直,如果存在,求线段
垂直,如果存在,求线段 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.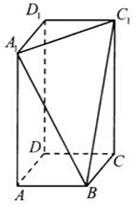
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西 处,受影响的范围是半径长为
处,受影响的范围是半径长为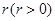 km的圆形区域.轮船的航行方向为西偏北
km的圆形区域.轮船的航行方向为西偏北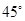 且不改变航线,假设台风中心不移动.如图所示,试问:
且不改变航线,假设台风中心不移动.如图所示,试问:
(1)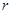 在什么范围内,轮船在航行途中不会受到台风的影响?
在什么范围内,轮船在航行途中不会受到台风的影响?
(2)当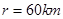 时,轮船在航行途中受到影响的航程是多少
时,轮船在航行途中受到影响的航程是多少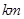 ?
?
在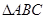 中,角
中,角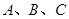 所对的边分别为
所对的边分别为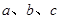 ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若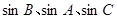 成等比数列,试判断
成等比数列,试判断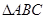 的形状.
的形状.
已知等差数列 的前
的前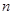 项和为
项和为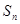 ,且
,且 ,
, ,在等比数列
,在等比数列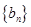 中,
中,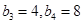 ,
,
(1)求 及
及 ;
;
(2)设数列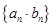 的前
的前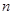 项和
项和 ,求
,求