在长方体 中,
中,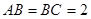 ,过
,过 ,
,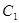 ,
, 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,这个几何体的体积为
,这个几何体的体积为 。
。
(1)证明:直线 ∥平面
∥平面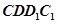 ;
;
(2)求棱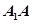 的长;
的长;
(3)在线段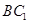 上是否存在点
上是否存在点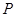 ,使直线
,使直线 与
与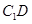 垂直,如果存在,求线段
垂直,如果存在,求线段 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.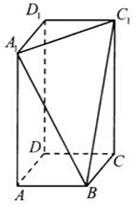
【2015高考湖北,文21】设函数 ,
, 的定义域均为
的定义域均为 ,且
,且 是奇函数,
是奇函数, 是偶函数,
是偶函数, ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(Ⅰ)求 ,
, 的解析式,并证明:当
的解析式,并证明:当 时,
时, ,
, ;
;
(Ⅱ)设 ,
, ,证明:当
,证明:当 时,
时, .
.
【2015高考广东,文21】(本小题满分14分)设 为实数,函数
为实数,函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)讨论 的单调性;
的单调性;
(3)当 时,讨论
时,讨论 在区间
在区间 内的零点个数.
内的零点个数.
【2015高考福建,文22】已知函数 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)证明:当 时,
时, ;
;
(Ⅲ)确定实数 的所有可能取值,使得存在
的所有可能取值,使得存在 ,当
,当 时,恒有
时,恒有 .
.
【2015高考北京,文19】(本小题满分13分)设函数 ,
, .
.
(Ⅰ)求 的单调区间和极值;
的单调区间和极值;
(Ⅱ)证明:若 存在零点,则
存在零点,则 在区间
在区间 上仅有一个零点.
上仅有一个零点.
【2015高考安徽,文21】已知函数
(Ⅰ)求 的定义域,并讨论
的定义域,并讨论 的单调性;
的单调性;
(Ⅱ)若 ,求
,求 在
在 内的极值.
内的极值.