如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准: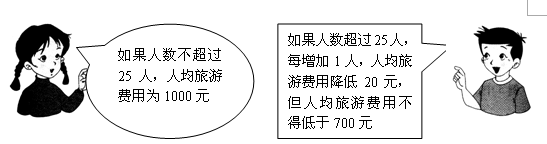 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余);
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
按上述分割方法进行下去……
(1)请你在下图中画出第一次分割的示意图;
(2)若原正六边形的面积为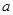 ,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
| 分割次数(n) |
1 |
2 |
3 |
…… |
| 正六边形的面积S |
(3)观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数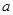 有何关系?(S用含
有何关系?(S用含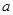 和n的代数式表示,不需要写出推理过程)。
和n的代数式表示,不需要写出推理过程)。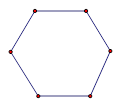
在平面直角坐标系中描出下列各点A(2,1),B(0,1),C(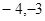 ),D(6,
),D(6,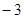 ),并将各点用线段一次连接构成一个四边形ABCD。
),并将各点用线段一次连接构成一个四边形ABCD。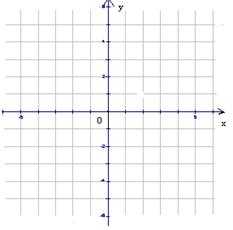
(1)四边形ABCD时什么特殊的四边形?
答:
(2)在四边形ABCD内找一点P,使得△APB、△BPC、△CPD、△APD都是等腰三角形,请写出P点的坐标。
小颖为九年级1班毕业联欢会设计了一个“配紫色“的游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,两个转盘停止转动时,若有一个转盘的指针指向蓝色,另一个转盘的指针指向红色,则”配紫色“成功,游戏者获胜,求游戏者获胜的概率。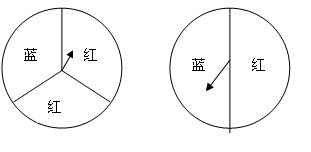
小刘对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2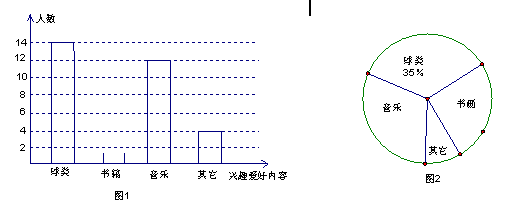
请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分的图形补充完整;
(2)在图2中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它“的人数占本班学生数的百分数;
(3)观察图1和图2,你能得出哪些结论?(只要写出一条结论)