（1）用分析法证明：当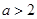
时，
；
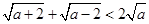（2）设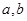
是两个不相等的正数，若
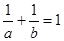，用综合法证明：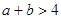
（本题8分）已知抛物线C：
和直线L：y =-2，直线L与y轴的交点D（0，-2），过点Q（0，2）的直线交抛物线C于A、B两点，与直线L交于点P．
（1）记
的面积为S，求S的取值范围；
（2）设
，
，求
的值。
（本题8分）已知几何体A—BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．
（1）求异面直线DE与AB所成角的余弦值；
（2）求二面角A-ED-B的正弦值；
（3）求此几何体的体积V的大小。
（本题8分）已知函数
．
（Ⅰ）当
时，求函数
的最小值和最大值;
（Ⅱ）设△ABC的对边分别为
，若
=
，
，
，求
的值．
（本题8分）已知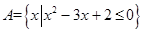集合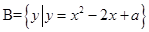
，集合
，集合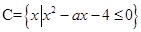
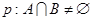．命题
，命题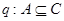
（Ⅰ）若命题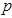
为假命题，求实数
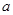的取值范围；
（Ⅱ）若命题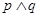
为真命题，求实数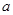的取值范围．
设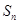
是等差数列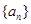
的前n项和，其中
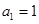，且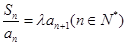
，
（Ⅰ）求常数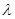
的值，并求数列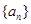的通项公式；
（Ⅱ）记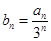
，设数列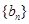
的前n项和为
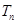，求最小的正整数
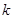，使得对任意的
，都有
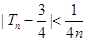成立．