已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再将图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位,再将图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数 的图象,求
的图象,求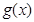 的最大值及取得最大值时的
的最大值及取得最大值时的 的集合
的集合
在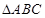 中,角
中,角 所对的边分别为
所对的边分别为 .
.
设向量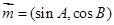 ,
,
(I)若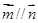 ,求角
,求角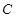 ;(Ⅱ)若
;(Ⅱ)若 ,
,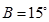 ,
,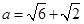 ,求边
,求边 的大小.
的大小.
已知公差不为零的等差数列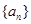 中,
中,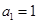 ,且
,且 成等比数列.
成等比数列.
(I)求数列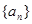 的通项公式; (II)设
的通项公式; (II)设 ,求数列
,求数列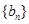 的前
的前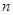 项和
项和 .
.
已知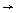
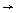
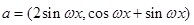 ,
,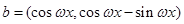 ,
,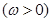 ,
,
函数 ,且函数
,且函数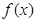 的最小正周期为
的最小正周期为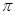 .
.
(I)求函数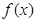 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数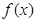 在
在 上的单调区间.
上的单调区间.
.设 :函数
:函数
 在区间
在区间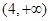 上单调递增;
上单调递增;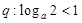 ,如果“
,如果“ ”是真命题,
”是真命题,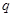 也是真命题,求实数
也是真命题,求实数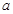 的取值范围.
的取值范围.
.已知定义在R上的二次函数 满足
满足 ,且
,且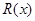 的最小值为0,函数
的最小值为0,函数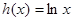 ,又函数
,又函数 。
。
(I)求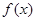 的单调区间;(II)当
的单调区间;(II)当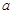 ≤
≤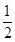 时,若
时,若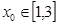 ,求
,求 的最小值;
的最小值;
(III)若二次函数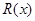 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数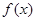 图象上的点A(
图象上的点A( ),
),
当 时,探求函数
时,探求函数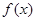 图象上是否存在点
图象上是否存在点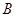 (
( )(
)(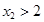 ),使
),使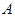 、
、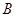 连线平行于
连线平行于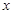 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…)