（本小题满分12分）设△ABC的内角A、B、C的对边长分别为a、b、c，设S为△ABC的面积，满足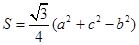
.
（Ⅰ）求B；
（Ⅱ）若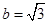
，设
，
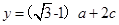，求函数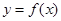
的解析式和最大值.
（本小题12分）
在人们对休闲方式的一次调
查中，共调查了124人，其中女性70人，男性54人。女性中有43人的休闲方式是看电视，27人的休闲方式是参加体育运动。男性中有21人的休闲方式是看电视，33人的休闲方式是参加体育运动。
（1）根据以上数据建立一个2×2的列联表
（2）判断性别是否与休闲方式有关系
（本小题10分）
证明：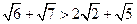
（本小题12分）
设函数
（1）若关于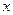
的方程
有三个不同的实根，求实数
的取值范围。
（2）当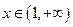
时，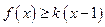
恒成立。求实数
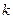的取值范围。
（本小题12分）
设函数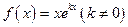
（1）求曲线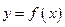
在点
处的切线方程。
（2）若函数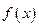
在区间
内单调递增，求
的取值范围。
（本小题12分）
若直线
分抛物线
与
轴所围成图形为面积相等的两部分，求
的值。 