已知函数f(x)= sin ωx-sin2
sin ωx-sin2 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值及函数f(x)的单调递增区间;
(2)当x∈ 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
由于某高中建设了新校区,为了交通方便要用三辆通勤车从新校区把教师接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(1)若三辆汽车中恰有一辆汽车被堵的概率为 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆汽车中被堵车辆的个数ξ的分布列和数学期望.
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.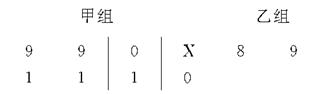
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差s2= [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
某活动将在辽宁沈阳举行,组委会在沈阳某大学招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm),身高在175 cm以上(包括175 cm)定义为“高个子”,身高在175 cm以下(不包括175 cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率;
(2)若从身高180 cm以上(包括180 cm)的志愿者中选出男、女各一人,求这2人身高相差5 cm以上的概率.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.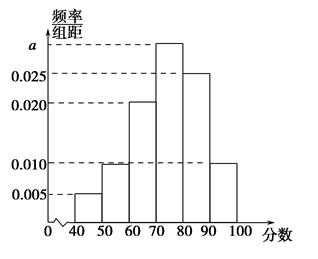
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.