(本小题满分16分)已知函数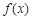 满足
满足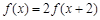 ,且当
,且当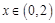 时,
时, ,当
,当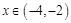 时,
时,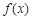 的最大值为
的最大值为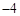 .
.
(1)求实数a的值;
(2)设 ,函数
,函数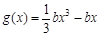 ,
,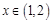 .若对任意
.若对任意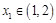 ,总存在
,总存在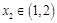 ,使
,使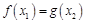 ,求实数b的取值范围.
,求实数b的取值范围.
(本小题满分12分)已知直线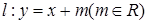 ,双曲线
,双曲线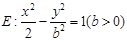 .①若直线
.①若直线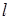 与双曲线
与双曲线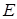 的其中一条渐近线平行,求双曲线
的其中一条渐近线平行,求双曲线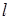 的离心率;②若直线
的离心率;②若直线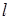 过双曲线的右焦点
过双曲线的右焦点 ,与双曲线交于
,与双曲线交于 、
、 两点,且
两点,且 ,求双曲线方程。
,求双曲线方程。
(本小题满分12分).已知椭圆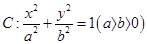 经过点
经过点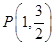 ,离心率
,离心率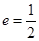 .
.
(Ⅰ)求椭圆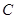 的方程;
的方程;
(Ⅱ)不过原点的直线 与椭圆
与椭圆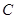 交于
交于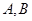 两点,若
两点,若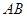 的中点
的中点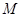 在抛物线
在抛物线 上,求直线
上,求直线 的斜率
的斜率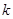 的取值范围.
的取值范围.
(本小题满分12分).已知双曲线 与椭圆
与椭圆 有共同的焦点,点
有共同的焦点,点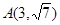 在双曲线
在双曲线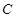 上.
上.
(Ⅰ)求双曲线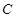 的方程;
的方程;
(Ⅱ)以 为中点作双曲线
为中点作双曲线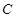 的一条弦
的一条弦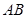 ,求弦
,求弦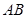 所在直线的方程.
所在直线的方程.
(本小题满分12分)已知圆 :
: ,直线
,直线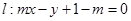
(Ⅰ)判断直线 与圆
与圆 的位置关系。
的位置关系。
(Ⅱ)若直线 与圆
与圆 交于不同两点
交于不同两点 ,且
,且 =3
=3 ,求直线
,求直线 的方程。
的方程。
(本小题满分10分)如图,已知过点 的光线,经
的光线,经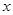 轴上一点
轴上一点 反射后的射线
反射后的射线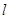 过点
过点 .
.
(1)求点 的坐标;
的坐标;
(2)若圆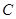 过点
过点 且与
且与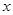 轴相切于点
轴相切于点 ,求圆
,求圆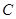 的方程.
的方程.