如图,益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)
(参考数据:sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80,sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50)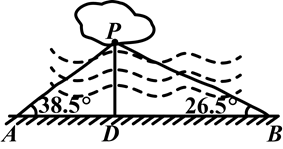
我市某中学艺术节期间,向全校学生征集书画作品.九年级美术王老师从全年级14个班中随机抽取了4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.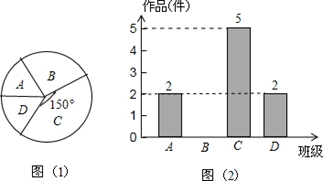
(1)王老师采取的调查方式是(填“普查”或“抽样调查”),王老师所调查的4个班征集到作品共件,其中B班征集到作品件,请把图2补充完整;
(2)王老师所调查的四个班平均每个班征集作品多少件?请估计全年级共征集到作品多少件?
(3)如果全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要在其中抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求写出用树状图或列表分析过程)
化简求值(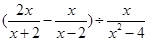 ,其中
,其中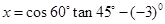 .
.
已知抛物线的顶点是C(0,m)(m>0,m为常数),并经过点(2m,2m),点D(0,2m)为一定点.
(1)求抛物线的解析式;(用含字母m的代数式表示)
(2)设点P是抛物线上任意一点,过P作PH⊥x轴,垂足是H,试探究PD与PH的大小关系,并说明理由;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且 =
= ,求m的值.
,求m的值.
已知直角坐标系中菱形ABCD的位置如图所示,C.D两点的坐标分别为 (4,0)、(0,3).现有两动点P、Q分别从A、C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为ts.
(1)菱形ABCD的边长是,面积是,高BE的长是.(直接填写结果)
(2)探究下列问题:
①若点P的速度为1cm/s,点Q的速度为2 cm/s.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式,以及S的最大值;
②若点P的速度为1cm/s,点Q的速度变为kcm/s,在运动过程中,任何时刻都有相应的k值,使得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形,请探究当t=4s时的情形,并求出k的值.
如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
(1)试判断BF与⊙O的位置关系,并说明理由;
(2)若BF=5, cos∠C= ,求⊙O的直径;
,求⊙O的直径;
(3)若cos∠F= ,则
,则 .(直接填写结果)
.(直接填写结果)