如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.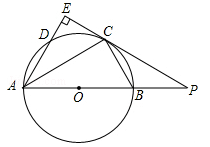
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
解答题△ABC外切于⊙O,切点分别为点D、E、F,∠A=60°,BC=7,⊙O的半径为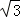 .
.
(1)求BF+CE的值;(2)求△ABC的周长.
解答题点D是△ABC内一点,AD平分∠ABC,延长AD交△ABC的外接圆于点E,BE=ED.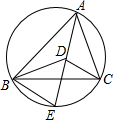
(1)点D是否是△ABC的内心?说明理由;
(2)点E是否是△BDC的外心?说明理由.
解答题如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.
(1)求证:BD=DI;
(2)若OI⊥AD,求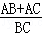 的值.
的值.
解答题已知抛物线y=x2﹣2x+m与x轴有两个不同交点A(x1,0)、B(x2,0)并且x1<x2,x12+x22=4,
①求这条抛物线的解析式;
②设抛物线的顶点为C,P是抛物线上一点,且∠PAC=90°,求P点坐标及△PAC内切圆的面积.
解答题如图,在△ABC中,O是内心,点E,F都在大边BC上,已知BF=BA,CE=CA.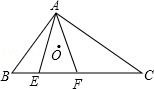
(1)求证:O是△AEF的外心;
(2)若∠B=40°,∠C=30°,求∠EOF的大小.