一个棱柱的直观图和三视图(主视图和俯视图是边长为 的正方形,左视图是直角边长为
的正方形,左视图是直角边长为 的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
的等腰三角形)如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.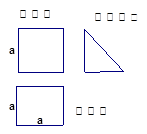
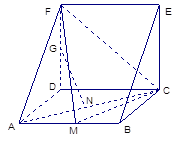
(Ⅰ)求证: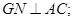
(Ⅱ)当FG=GD时,证明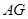 //平面FMC;
//平面FMC;
(Ⅲ)求三棱锥 的体积
的体积
50件产品中有3件次品,不放回地抽取2次,每次抽1件,已知第1次抽出的是次品,求第2次抽出的也是次品的概率.
为防止某突发事件,有甲、乙、丙、丁四种相互独立的预防措施可供采用,单独采用甲、乙、丙、丁预防措施后突发事件不发生的概率(记为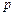 )和所需费如下表:
)和所需费如下表:
| 预防措施 |
甲 |
乙 |
丙 |
丁 |
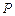 |
0.9 |
0.8 |
0.7 |
0.6 |
| 费用(万元) |
90 |
60 |
30 |
10 |
预防方案可单独采用一种预防措施或联合采用几种预防措施.在总费不超过120万元的前提下,请确定一个预防方案,使得此突发事件不发生的概率最大.
一个口袋中装有若干个均匀的红球和白球,从中摸出一个红球的概率是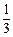 .有放回地摸球,每次摸出一个,有3次摸到红球即停止.
.有放回地摸球,每次摸出一个,有3次摸到红球即停止.
(1)求恰好摸5次停止的概率;
(2)记5次之内(含5次)摸到红球的次数为X,求随机变量X的分布列.
某人提出一问题,甲先答,答对的概率为0.6,如果甲答错,由乙答,乙答对的概率是0.7,求由乙解出该问题的概率.
已知 的边
的边 上有5个点,边OB上有6个点,用这些点和O点为顶点,能构成多少个不同的三角形?
上有5个点,边OB上有6个点,用这些点和O点为顶点,能构成多少个不同的三角形?