(本小题满分12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| |
“厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为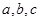 ,其中
,其中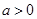 ,
, .当数据
.当数据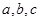 的方差
的方差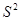 最大时,写出
最大时,写出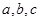 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时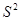 的值.(注:方差
的值.(注:方差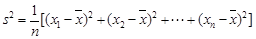 ,其中
,其中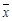 为
为 的平均数)
的平均数)
已知数列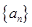 的首项
的首项 的等比数列,其前
的等比数列,其前 项和
项和 中
中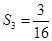 ,
,
(1)求数列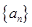 的通项公式;
的通项公式;
(2)设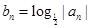 ,
, ,求证:
,求证:
已知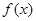
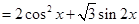
(Ⅰ)求函数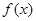 的单调递增区间;
的单调递增区间;
(Ⅱ)在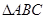 中,
中,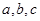 分别是角A,B,C的对边,
分别是角A,B,C的对边,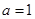 且
且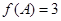 ,求
,求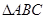 的面积
的面积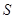 的最大值.
的最大值.
已知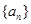 是公比大于1的等比数列,
是公比大于1的等比数列,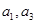 是函数
是函数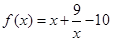 的两个零点。
的两个零点。
(1)求数列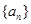 的通项公式;
的通项公式;
(2)若数列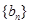 满足
满足 ,且
,且 ,求
,求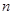 的最小值。
的最小值。
(本小题满分14分)(注意:在试题卷上作答无效)
已知曲线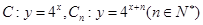 ,从
,从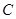 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交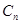 于点
于点 ,再从点
,再从点 作
作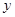 轴的垂线,交
轴的垂线,交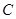 于点
于点 ,设
,设
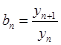
(1)求数列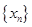 的通项公式;
的通项公式;
(2)记 ,数列
,数列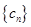 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小
的大小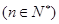 ;
;
(3)记 ,数列
,数列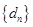 的前
的前 项和为
项和为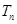 ,试证明:
,试证明:

(本小题14分,计入总分)
已知数列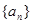 满足:
满足: 
⑴求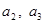 ;
;
⑵当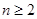 时,求
时,求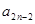 与
与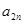 的关系式,并求数列
的关系式,并求数列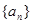 中偶数项的通项公式;
中偶数项的通项公式;
⑶求数列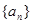 前100项中所有奇数项的和.
前100项中所有奇数项的和.