(本小题满分10分)选修4-4:坐标系与参数方程
曲线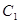 的参数方程为
的参数方程为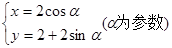 ,
,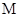 是曲线
是曲线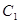 上的动点,且
上的动点,且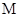 是线段
是线段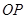 的中点,
的中点,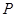 点的轨迹为曲线
点的轨迹为曲线 ,直线l的极坐标方程为
,直线l的极坐标方程为 ,直线l与曲线
,直线l与曲线 交于
交于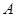 ,
,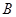 两点。
两点。
(Ⅰ)求曲线 的普通方程;
的普通方程;
(Ⅱ)求线段 的长。
的长。
已知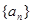 是单调递增的等差数列,首项
是单调递增的等差数列,首项 ,前
,前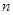 项和为
项和为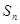 ,数列
,数列 是等比数列,首项
是等比数列,首项
(1)求 和
和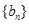 的通项公式.
的通项公式.
(2)设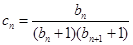 ,数列
,数列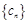 的前
的前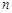 项和为
项和为 ,求证:
,求证: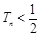 .
.
已知函数 (其中
(其中 ,
, ,
,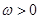 )的最大值为2,最小正周期为
)的最大值为2,最小正周期为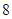 .
.
(1)求函数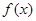 的解析式;
的解析式;
(2)若函数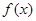 图象上的两点
图象上的两点 的横坐标依次为
的横坐标依次为 ,
,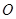 为坐标原点,求
为坐标原点,求 的值.
的值.
为了解《中华人民共国道路交通安全法》在学生中的普及情况,调查部门对某学校6名学生进行问卷调查,6人得分情况如下:
5,6,7,8,9,10。
把这6名学生的得分看成一个总体。
(1)求该总体的平均数;
(2)求该总体的的方差;
(3)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本,求该样本平均数于总体平均数之差的绝对值不超过0.5的概率。
若以连续掷两次骰子分别得到的点数m、n作为点P的坐标 ,求:
,求:
(1)点P在直线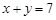 上的概率;
上的概率;
(2)点P在圆 外的概率。
外的概率。
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为 和
和 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.