甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为 和
和 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是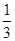 ,每次测试通过与否相互独立.规定:若前4次都没有通过测试,则第5次不能参加测试.
,每次测试通过与否相互独立.规定:若前4次都没有通过测试,则第5次不能参加测试.
(1)求该学生考上大学的概率;
(2)如果考上大学或参加完5次考试就结束,求该生至少参加四次考试的概率
已知数列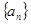 的前
的前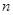 项和,
项和,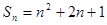 。
。
(I)求数列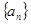 的通项公式
的通项公式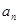 ;
;
(II)记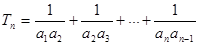 ,求
,求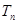
已知函数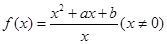 是奇函数,且满足
是奇函数,且满足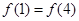
(Ⅰ)求实数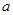 、
、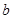 的值;
的值;
(Ⅱ)试证明函数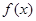 在区间
在区间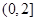 单调递减,在区间
单调递减,在区间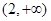 单调递增;
单调递增;
(Ⅲ)是否存在实数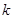 同时满足以下两个条件:1不等式
同时满足以下两个条件:1不等式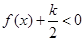 对
对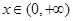 恒成立; 2方程
恒成立; 2方程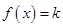 在
在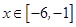 上有解.若存在,试求出实数
上有解.若存在,试求出实数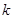 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
已知函数 (
( 为实常数).
为实常数).
(1)若 ,求
,求 的单调区间;
的单调区间;
(2)若 ,设
,设 在区间
在区间 的最小值为
的最小值为 ,求
,求 的表达式;
的表达式;
(3)设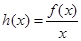 ,若函数
,若函数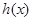 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h),可以把这批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700].由于工作中不慎将部分数据丢失,现有以下部分图表: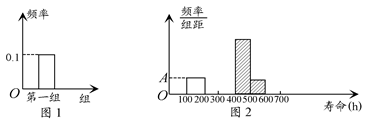
| 分组 |
[100,200] |
(200,300] |
(300,400] |
(400,500] |
(500,600] |
(600,700] |
| 频数 |
B |
30 |
E |
F |
20 |
H |
| 频率 |
C |
D |
0.2 |
0.4 |
G |
I |
(1)求图2中的A及表格中的B,C,D,E,F,G,H,I的值;
(2)求图2中阴影部分的面积;
(3)若电子元件的使用时间超过300h为合格产品,求这批电子元件合格的概率.