已知椭圆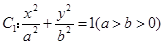 的一条准线方程是
的一条准线方程是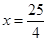 ,其左、右顶点分别是A、B;双曲线
,其左、右顶点分别是A、B;双曲线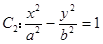 的一条渐近线方程为
的一条渐近线方程为 .
.
(1)求椭圆 的方程及双曲线
的方程及双曲线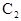 的离心率;
的离心率;
(2)在第二象限内取双曲线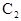 上一点P,连结BP交椭圆
上一点P,连结BP交椭圆 于点M,连结PA并延长交椭圆
于点M,连结PA并延长交椭圆 于点N,若
于点N,若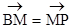 .求证:
.求证: .
.
若函数f(x)=ax3+bx2+cx+d是奇函数,且
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
若函数f(x)=ax3+bx2+cx+d是奇函数,且f(x)极小值=f(-)=-.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
设
(1)求点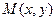 的轨迹C的方程;
的轨迹C的方程;
(2)过点 的直线
的直线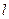 交曲线C于A,B两点(A在P,B之间),设
交曲线C于A,B两点(A在P,B之间),设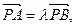 直线
直线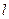 的斜率为k,当
的斜率为k,当 时,求实数
时,求实数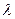 的取值范围。
的取值范围。
已知 是定义在
是定义在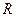 上的函数,且满足下列条件:
上的函数,且满足下列条件:
①对任意的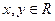 ,
,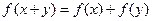 ;②当
;②当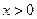 时,
时, .
.
(1)证明 是定义在
是定义在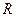 上的减函数;
上的减函数;
(2)如果对任意实数 ,有
,有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知平面区域 恰好被面积最小的圆
恰好被面积最小的圆 及其内
及其内
部所覆盖.(1)试求圆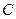 的方程.
的方程.
(2)若斜率为1的直线 与圆C交于不同两点
与圆C交于不同两点 满足
满足 ,求直线
,求直线 的方程.
的方程.