已知 是定义在
是定义在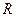 上的函数,且满足下列条件:
上的函数,且满足下列条件:
①对任意的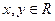 ,
,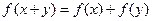 ;②当
;②当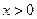 时,
时, .
.
(1)证明 是定义在
是定义在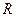 上的减函数;
上的减函数;
(2)如果对任意实数 ,有
,有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
在二项式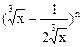 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列
(1)求展开式的第四项;
(2)求展开式的常数项;
(3)求展开式中各项的系数和.
如图,圆柱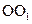 内有一个三棱柱
内有一个三棱柱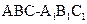 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。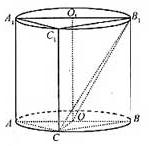
(Ⅰ)证明:平面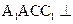 平面
平面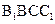 ;
;
(Ⅱ)设AB=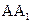 ,在圆柱
,在圆柱 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱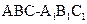 内的概率为
内的概率为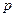 。
。
(i)当点C在圆周上运动时,求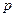 的最大值;
的最大值;
(ii)记平面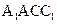 与平面
与平面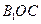 所成的角为
所成的角为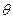
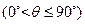 ,当
,当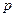 取最大值时,求
取最大值时,求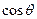 的值。
的值。
设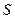 是不等式
是不等式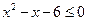 的解集,整数
的解集,整数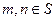 。
。
(1)记使得“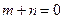 成立的有序数组
成立的有序数组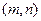 ”为事件A,试列举A包含的基本事件;
”为事件A,试列举A包含的基本事件;
(2)设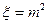 ,求
,求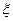 的分布列及其数学期望
的分布列及其数学期望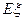 。
。
已知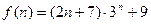 是否存在自然数
是否存在自然数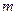 ,使对任意
,使对任意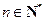 ,都有
,都有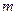 整除
整除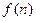 ?如果存在,求出
?如果存在,求出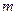 的最大值,并证明;若不存在,说明理由.
的最大值,并证明;若不存在,说明理由.
、某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是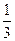 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(2)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
(3)求这名学生在上学路上因遇到红灯停留的总时间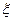 的分布列、期望及方差
的分布列、期望及方差