图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.
如图1,在平面直角坐标系中,点 的坐标是 ,在 轴上任取一点 ,连接 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 ,过点 作 轴的垂线 交直线 于点 .根据以上操作,完成下列问题.
探究:
(1)线段 与 的数量关系为 ,其理由为: .
(2)在 轴上多次改变点 的位置,按上述作图方法得到相应点 的坐标,并完成下列表格:
|
的坐标 |
|
|
|
|
|
|
|
的坐标 |
|
|
|
|
|
|
猜想:
(3)请根据上述表格中 点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线 ,猜想曲线 的形状是 .
验证:
(4)设点 的坐标是 ,根据图1中线段 与 的关系,求出 关于 的函数解析式.
应用:
(5)如图3,点 , ,点 为曲线 上任意一点,且 ,求点 的纵坐标 的取值范围.
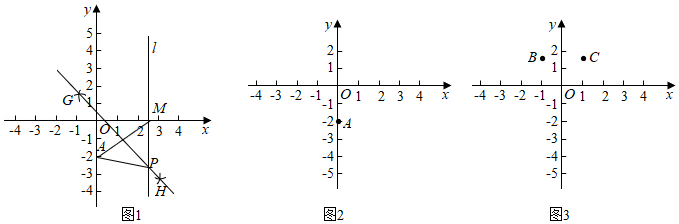
问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

小刚去超市购买画笔,第一次花60元买了若干支 型画笔,第二次超市推荐了 型画笔,但 型画笔比 型画笔的单价贵2元,他又花100元买了相同支数的 型画笔.
(1)超市 型画笔单价多少元?
(2)小刚使用两种画笔后,决定以后使用 型画笔,但感觉其价格稍贵,和超市沟通后,超市给出以下优惠方案:一次购买不超过20支,则每支 型画笔打九折;若一次购买超过20支,则前20支打九折,超过的部分打八折.设小刚购买的 型画笔 支,购买费用为 元,请写出 关于 的函数关系式.
(3)在(2)的优惠方案下,若小刚计划用270元购买 型画笔,则能购买多少支 型画笔?
如图,点 在以 为直径的 上,点 是半圆 的中点,连接 , , , .过点 作 交 的延长线于点 .
(1)求证:直线 是 的切线;
(2)若 , ,求 , 的长.

如图,无人机在离地面60米的 处,观测楼房顶部 的俯角为 ,观测楼房底部 的俯角为 ,求楼房的高度.
