通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由 得,
得, .
.
附表:
 |
0.050 |
0.010 |
0.001 |
 |
3.841 |
6.635 |
10.828 |
参照附表,下列结论正确的是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
已知直线l的参数方程是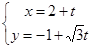 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 .
.
(1)求曲线C的直角坐标方程和参数方程;
(2)求直线l被曲线C截得的弦长.
我们把一系列向量 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作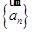 ,已知向量列
,已知向量列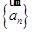 满足:
满足: ,
,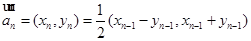
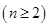 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)设 表示向量
表示向量 与
与 间的夹角,若
间的夹角,若 ,对于任意正整数
,对于任意正整数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的范围;
的范围;
(3)设 ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
袋子中放有大小和形状相同的小球若干,其中标号为1的小球1个,标号为2的小球2个,标号为3的小球 个,已知从袋中随机抽取1个小球,取到标号3的小球的概率为
个,已知从袋中随机抽取1个小球,取到标号3的小球的概率为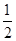 .
.
(1)求 的值;
的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出的小球标号为 ,第二次取出的小球标号为
,第二次取出的小球标号为 .
.
①记“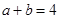 ”为事件A,求事件A的概率;
”为事件A,求事件A的概率;
②在区间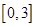 内任取2个实数
内任取2个实数 ,求事件“
,求事件“ ” 恒成立的概率.
” 恒成立的概率.
已知命题 .命题
.命题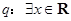 ,使得
,使得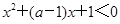 .若
.若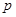 或
或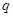 为真,
为真,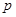 且
且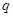 为假,求实数a的取值范围.
为假,求实数a的取值范围.
对某电子元件进行寿命追踪调查,所得情况如右频率分布直方图.
(1)图中纵坐标 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 ;
;
(2)根据图表的数据按分层抽样,抽取 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率.