如图，已知抛物线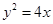
，点
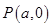是x轴上的一点，经过点
且斜率为1的直线
与抛物线相交于
两点．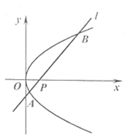
（1）求证线段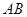
的中点在一条定直线上，并求出该直线方程；
（2）若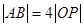
（O为坐标原点），求
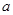的值．
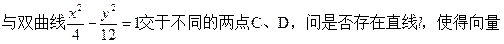
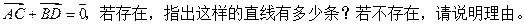
已知直线l的方程为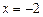
，且直线l与x轴交于点M，圆
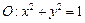与x轴交于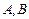
两点（如图）．
（I）过M点的直线
交圆于
两点，且圆孤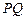
恰为圆周的
，求直线的方程；
（II）求以l为准线，中心在原点，且与圆O恰有两个公共点的椭圆方程；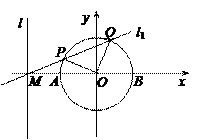
（III）过M点的圆的切线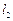
交（II）中的一个椭圆于
两点，其中两点在x轴上方，求线段CD的长．
一圆形纸片的半径为10cm，圆心为O，F为圆内一定点，OF=6cm，M为圆周上任意一点，把圆纸片折叠，使M与F重合，然后抹平纸片，这样就得到一条折痕CD，设CD与OM交于P点，如图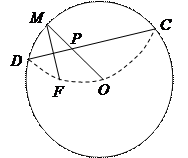
（1）求点P的轨迹方程；
（2）求证：直线CD为点P轨迹的切线.
已知点A、B的坐标分别是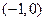
，
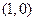.直线
相交于点M，且它们的斜率之积为－2.
(Ⅰ)求动点M的轨迹方程;
(Ⅱ)若过点
的直线
交动点M的轨迹于C、D两点, 且N为线段CD的中点，求直线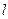的方程.
已知抛物线的顶点为椭圆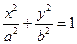
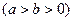的中心.椭圆的离心率是抛物线离心率的一半，且它们的准线互相平行。又抛物线与椭圆交于点
，求抛物线与椭圆的方程.