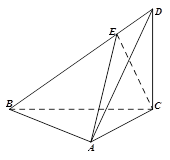
如图,在矩形ABCD中,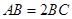 ,
,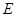 为
为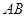 上一点,以直线EC为折线将点B折起至点P,并保持∠PEB为锐角,连结PA、PC、PD,取PD的中点F,若有AF∥平面PEC。
上一点,以直线EC为折线将点B折起至点P,并保持∠PEB为锐角,连结PA、PC、PD,取PD的中点F,若有AF∥平面PEC。
(Ⅰ)试确定点E的位置;
(Ⅱ)若异面直线PE、CD所成的角为60°,求证:平面PEC⊥平面AECD。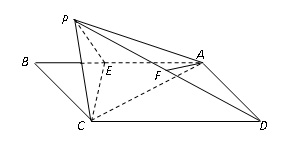
已知定义在R上的函数f(x) 同时满足:①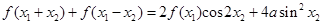 (
( R,a为常数);②
R,a为常数);②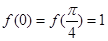 ;③当
;③当 时,
时, ≤2。
≤2。
求:(Ⅰ)函数 的解析式;(Ⅱ)常数a的取值范围。
的解析式;(Ⅱ)常数a的取值范围。
设函数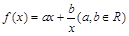 ,若
,若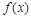 在点
在点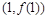 处的切线斜率为
处的切线斜率为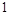 .
.
(Ⅰ)用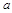 表示
表示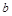 ;
;
(Ⅱ)设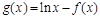 ,若
,若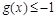 对定义域内的
对定义域内的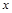 恒成立,
恒成立,
(ⅰ)求实数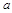 的取值范围;
的取值范围;
(ⅱ)对任意的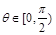 ,证明:
,证明: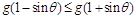 .
.
设点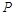 为圆
为圆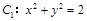 上的动点,过点
上的动点,过点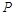 作
作 轴的垂线,垂足为
轴的垂线,垂足为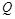 .动点
.动点 满足
满足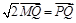 (其中
(其中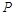 ,
,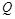 不重合).
不重合).
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过直线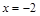 上的动点
上的动点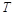 作圆
作圆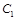 的两条切线,设切点分别为
的两条切线,设切点分别为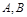 .若直线
.若直线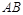 与(Ⅰ)中的曲线
与(Ⅰ)中的曲线 交于
交于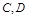 两点,求
两点,求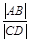 的取值范围.
的取值范围.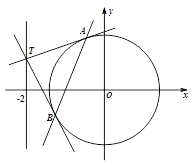
如图,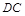 垂直平面
垂直平面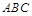 ,
,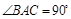 ,
,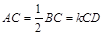 ,点
,点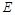 在
在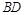 上,且
上,且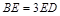 .
.
(Ⅰ)求证: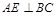 ;
;
(Ⅱ)若二面角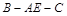 的大小为
的大小为 ,求
,求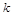 的值.
的值.