某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
| 单价(元/件) |
30 |
34 |
38 |
40 |
42 |
| 销量(件) |
40 |
32 |
24 |
20 |
16 |
(1)计算这5天销售额的平均数(销售额=单价 销量)
销量)
(2)通过对上面表格中的数据进行分析,发现销量 (件)与单价
(件)与单价 (元/件)之间存在一次函数关系,求
(元/件)之间存在一次函数关系,求 关于
关于 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围);
(3)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
解方程
(1)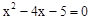 (配方法)(2)
(配方法)(2)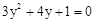 (公式法)
(公式法)
在平面直角坐标系xOy中,点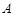 、
、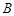 分别在
分别在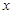 轴、
轴、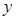 轴的正半轴上,且
轴的正半轴上,且 ,点
,点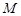 为线段
为线段 的中点.
的中点.
(1)如图1,线段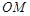 的长度为________________;
的长度为________________;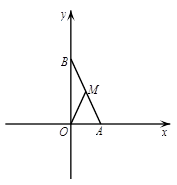
(2)如图2,以 为斜边作等腰直角三角形
为斜边作等腰直角三角形 ,当点
,当点 在第一象限时,求直线
在第一象限时,求直线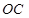 所对应的函数的解析式;
所对应的函数的解析式;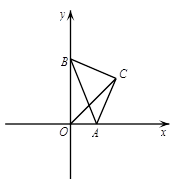
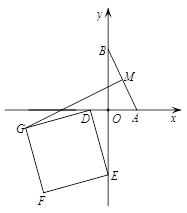
(3)如图3,设点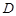 、
、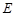 分别在
分别在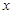 轴、
轴、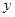 轴的负半轴上,且
轴的负半轴上,且 ,以
,以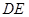 为边在第三象限内作正方形
为边在第三象限内作正方形 ,请求出线段
,请求出线段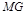 长度的最大值,并直接写出此时直线
长度的最大值,并直接写出此时直线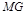 所对应的函数的解析式.
所对应的函数的解析式.
|
已知在 中,
中,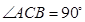 ,
,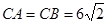 ,
, 于
于 ,点
,点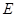 在直线
在直线 上,
上, ,点
,点 在线段
在线段 上,
上, 是
是 的中点,直线
的中点,直线 与直线
与直线 交于
交于 点.
点.
(1)如图1,若点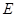 在线段
在线段 上,请分别写出线段
上,请分别写出线段 和
和 之间的位置关系和数量关系:___________,___________;
之间的位置关系和数量关系:___________,___________;

(2)在(1)的条件下,当点 在线段
在线段 上,且
上,且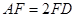 时,求证:
时,求证: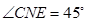 ;
;
(3)当点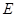 在线段
在线段 的延长线上时,在线段
的延长线上时,在线段 上是否存在点
上是否存在点 ,使得
,使得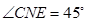 .若存在,请直接写出
.若存在,请直接写出 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
已知关于 的一元二次方程
的一元二次方程 .
.
(1)求证:此方程总有两个实数根;
(2)若此方程的两个实数根都是整数,求 的整数值;
的整数值;
(3)若此方程的两个实数根分别为 、
、 ,求代数式
,求代数式 的值.
的值.
阅读下面的材料:
小明在研究中心对称问题时发现:
如图1,当点 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点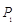 再绕着点
再绕着点 旋转180°得到
旋转180°得到 点,这时点
点,这时点 与点
与点 重合.
重合.
如图2,当点 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到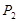 点,点
点,点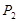 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到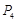 点,小明发现P、
点,小明发现P、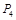 两点关于点
两点关于点 中心对称.
中心对称.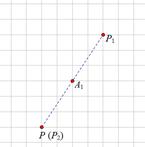


(1)请在图2中画出点 、
、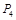 , 小明在证明P、
, 小明在证明P、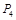 两点关于点
两点关于点 中心对称时,除了说明P、
中心对称时,除了说明P、 、
、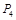 三点共线之外,还需证明;
三点共线之外,还需证明;
(2)如图3,在平面直角坐标系xOy中,当 、
、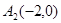 、
、 为旋转中心时,点
为旋转中心时,点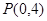 绕着点
绕着点 旋转180°得到
旋转180°得到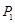 点;点
点;点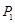 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到点
旋转180°得到点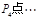 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点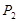 的坐标为(),点
的坐标为(),点 的坐为.
的坐为.