(本小题满分12分)下图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80-90分数段的学员数为21人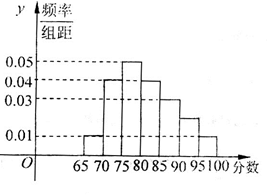
(1)求该专业毕业总人数N和90-95分数段内的人数 ;
;
(2)现欲将90-95分数段内的 名人分配到几所学校,从中安排2人到甲学校去,若
名人分配到几所学校,从中安排2人到甲学校去,若 人中仅有两名男生,求安排结果至少有一名男生的概率.
人中仅有两名男生,求安排结果至少有一名男生的概率.
已知函数 , ,其中 a>1.
(I)求函数 的单调区间;
(II)若曲线 在点 处的切线与曲线 在点 处的切线平行,证明 ;
(III)证明当 时,存在直线 l,使 l是曲线 的切线,也是曲线 的切线.
设椭圆 (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为 ,点A的坐标为 ,且 .
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l: 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若 (O为原点) ,求k的值.
设 是等比数列,公比大于0,其前n项和为 , 是等差数列.已知 , , , .
(I)求 和 的通项公式;
(II)设数列 的前n项和为 ,
(i)求 ;
(ii)证明 .
如图, 且AD=2BC, , 且EG=AD, 且CD=2FG, ,DA=DC=DG=2.
(Ⅰ)若M为CF的中点,N为EG的中点,求证: ;
(Ⅱ)求二面角 的正弦值;
(Ⅲ)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.

已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.