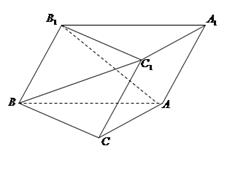
如图,斜三棱柱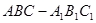 的底面是直角三角形,
的底面是直角三角形,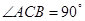 ,点
,点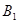 在底面内的射影恰好是
在底面内的射影恰好是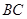 的中点,且
的中点,且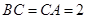 .
.
(1)求证:平面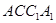
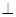 平面
平面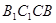 ;
;
(2)若二面角 的余弦值为
的余弦值为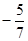 ,求斜三棱柱
,求斜三棱柱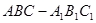 的侧棱
的侧棱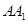 的长度.
的长度.
设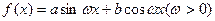 的周期
的周期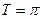 ,最大值
,最大值 ,
,
(1)求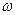 、
、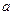 、
、 的值;
的值;
(2) .
.
实数 满足
满足 求
求 的值.
的值.
已知函数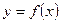 的图象关于直线
的图象关于直线 对称,当
对称,当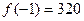 ,
,
且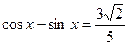 时,试求
时,试求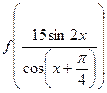 的值.
的值.
如图,在锐角△ABC中,AB<AC,AD是边BC上的高,P是线段AD内一点。过P作PE⊥AC,垂足为E,做PF⊥AB,垂足为F。O1、O2分别是△BDF、△CDE的外心。求证:O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。
设函数f(x)对所有的实数x都满足f(x+2π)=f(x),求证:存在4个函数fi(x)(i=1,2,3,4)满足:(1)对i=1,2,3,4,fi(x)是偶函数,且对任意的实数x,有fi(x+π)=fi(x);(2)对任意的实数x,有f(x)=f1(x)+f2(x)cosx+f3(x)sinx+f4(x)sin2x。