已知函数f（x）=4cos2x﹣4
sinxcosx﹣2（x∈R）．
（1）求函数f（x）的单调递增区间；
（2）设△ABC的内角A，B，C对应边分别为a、b、c，且c=3，f（C）=﹣4，若向量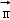
=（1，sinA）与向量
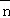=（1，2sinB）共线，求a、b的值．
如图,四棱锥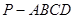
的底面是边长为
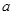的菱形,
,
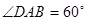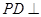平面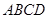
,
.
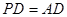（1）求直线PB与平面PDC所成的角的正切值;
（2）求二面角A－PB－D的大小.
（本小题满分12分）
已知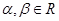
，写出用
表示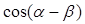
的关系等式，并证明这个关系等式．
（本小题满分10分）
如图，在直三棱柱
中，
，
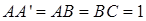．棱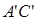
上有两个动点E，F，且EF =" a" （a为常数）．
（Ⅰ）在平面ABC内确定一条直线，使该直线与直线CE垂直；
（Ⅱ）判断三棱锥B—CEF的体积是否为定值．若是定值，求出这个三棱锥的体积；若不是定值，说明理由．
（本小题满分10分）
记等差数列{
}的前n项和为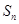
，已知
，
．
（Ⅰ）求数列{}的通项公式；
（Ⅱ）令
，求数列{
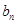}的前项和
．
（本小题满分10分）
一种放射性元素，最初的质量为500g，按每年10﹪衰减．
（Ⅰ）求t年后，这种放射性元素质量ω的表达式；
（Ⅱ）由求出的函数表达式，求这种放射性元素的半衰期（剩留量为原来的一半所需要的时间）．（精确到0．1；参考数据：
）