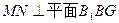(本小题满分12分)如图,直三棱柱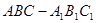 的底面是边长为
的底面是边长为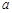 的正三角形,点M在边BC上,
的正三角形,点M在边BC上, 是以M为直角顶点的等腰直角三角形.
是以M为直角顶点的等腰直角三角形.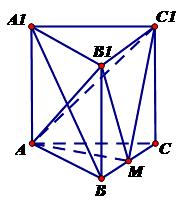
(1)求证:直线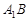 ∥平面
∥平面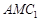 ;
;
(2)求三棱锥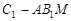 的高
的高
甲、乙等五名奥运志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者
(1)求甲、乙两人同时参加A岗位服务的概率
(2)求甲、乙两人不在同一个岗位服务的概率
(3)设随机变量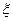 为这5名志愿者中参加A岗位服务的人数,求
为这5名志愿者中参加A岗位服务的人数,求
已知函数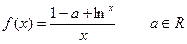
(1)求 的极值
的极值
(2)若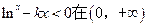 上恒成立,求
上恒成立,求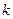 的取值范围
的取值范围
(3)已知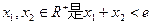 ,求证:
,求证: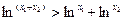
斜率为1的直线过抛物线 的焦点,与抛物线交于两点A、B将直线AB接向量
的焦点,与抛物线交于两点A、B将直线AB接向量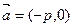 平移得直线
平移得直线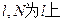 的动点,M为抛物线弧AB上的动点
的动点,M为抛物线弧AB上的动点
①若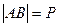 ,求抛物线方程
,求抛物线方程
②求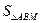 的最大值
的最大值
③求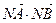 的最小值
的最小值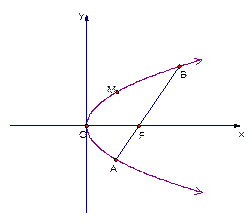
设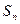 是正项数列
是正项数列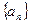 的前n项和且
的前n项和且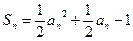
(1)求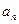 (2)
(2)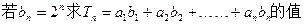
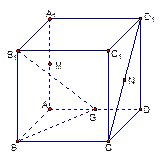
如图在正方体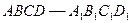 中,M、N、G分别是
中,M、N、G分别是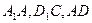 的中点
的中点
(1)判断直线 与平面
与平面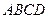 的位置关系,并证明你的结论
的位置关系,并证明你的结论
(2)求证