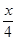已知抛物线
与x轴交于点A（m－2，0）和B（2m＋1，0）（点A在点B的左侧），与y轴相交于点C，顶点为P，对称轴为l：x＝1．
（1）求抛物线解析式．
（2）直线y＝kx＋2（k≠0）与抛物线相交于两点M（x1，y1），N（x2，y2）（x1＜x2），当 
最小时，求抛物线与直线的交点M和N的坐标．
（3）首尾顺次连接点O，B，P，C构成多边形的周长为L．若线段OB在x轴上移动，求L最小值时点O，B移动后的坐标及L的最小值．
（如图，已知∠AOB=ll0°，∠AOC=m∠AOD，∠COE=n∠BOC，且3（m－2）＋4=m＋2，单项式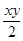
的系数为n．
（1）求4(m-n) 2-(m-n) 2-5的值；
（2）当∠COD：∠COE=3：2时，试求∠COD的度数.
如图，点A、B.、C在同一条直线上，D为AC的中点，且AB=6cm，BC=2cm．
(1)试求AD的长；
(2)求AD：BD的值。
将一副三角尺按照如图的位置摆放，使得三角尺ACB的直角顶点C在三角尺DEF的直角边EF上．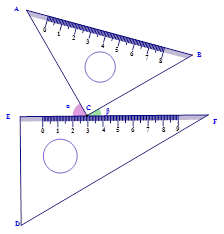
(1)求∠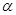
十∠
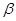的度数；
(2)若∠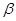=32°，试问∠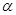的补角为多少度？
先化简后求值，2x-5(x-2y)+6x(1-3y)，其中x=4，y=-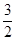
解方程：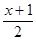
=2+