(本小题13分)设全集 ,已知函数
,已知函数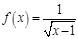 的定义域为集合
的定义域为集合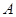 ,函数
,函数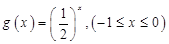 的值域为集合
的值域为集合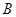 .
.
(1)求 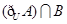 ;
;
(2)若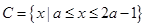 且
且 ,求实数
,求实数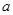 的取值范围.
的取值范围.
解关于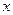 的不等式:
的不等式: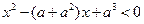
(本小题12分)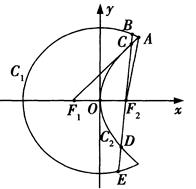
如图,曲线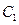 是以原点
是以原点 为中心,以
为中心,以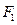 、
、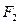 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线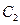 是以
是以 为顶点,以
为顶点,以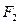 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, 是曲线
是曲线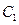 和
和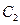 的交点,且
的交点,且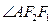 为钝角,若
为钝角,若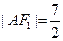 ,
,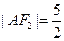 .
.
(I)求曲线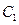 和
和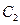 所在的椭圆和抛物线的方程;
所在的椭圆和抛物线的方程;
(II)过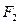 作一条与轴不垂直的直线,分别与曲线
作一条与轴不垂直的直线,分别与曲线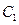 、
、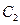 依次交于
依次交于 、
、 、
、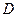 、
、 四点(如图),若
四点(如图),若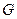 为
为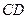 的中点,
的中点,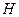 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
(本小题14分)
设函数 ,其中
,其中 .
.
(I)当 时,判断函数
时,判断函数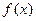 在定义域上的单调性;
在定义域上的单调性;
(II)求函数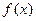 的极值点;
的极值点;
(III)证明对任意的正整数 ,不等式
,不等式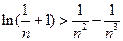 都成立.
都成立.
(本小题13分)
设等比数列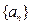 的前项和为
的前项和为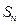 ,首项
,首项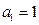 ,公比
,公比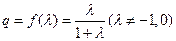 .
.
(I)证明: ;
;
(II)若数列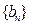 满足
满足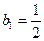 ,
,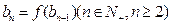 ,求数列
,求数列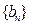 的通项公式;
的通项公式;
(III)记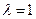 ,
,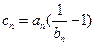 ,数列
,数列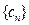 的前项和为
的前项和为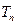 ,求证:当
,求证:当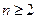 时,
时, .
.
(本小题12分)
为了拓展网络市场,腾讯公司为QQ用户推出了多款QQ应用,如“QQ农场”、“QQ音乐”、“QQ读书”等.市场调查表明,QQ用户在选择以上三种应用时,选择农场、音乐、读书的概率分别为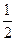 ,
,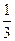 ,
,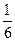 .现有甲、乙、丙三位QQ用户独立任意选择以上三种应用中的一种进行添加.
.现有甲、乙、丙三位QQ用户独立任意选择以上三种应用中的一种进行添加.
(I)求三人所选择的应用互不相同的概率;
(II)记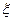 为三人中选择的应用是QQ农场与QQ音乐的人数,求
为三人中选择的应用是QQ农场与QQ音乐的人数,求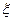 的分布列与数学期望.
的分布列与数学期望.