【2015高考山东,文21】平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: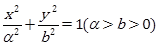 的离心率为
的离心率为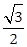 ,且点(
,且点( ,
,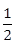 )在椭圆
)在椭圆 上.
上.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆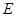 :
: ,
, 为椭圆
为椭圆 上任意一点,过点
上任意一点,过点 的直线
的直线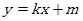 交椭圆
交椭圆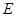 于
于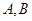 两点,射线
两点,射线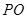 交椭圆
交椭圆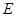 于点
于点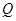 .
.
(ⅰ)求 的值;
的值;
(ⅱ)求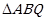 面积的最大值.
面积的最大值.
 在△ABC
在△ABC 中,已知
中,已知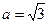 ,
,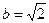 ,B=45°, 求A、C及c
,B=45°, 求A、C及c
(本小题满分12分)
设函数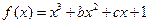 的单调减区间是(1,2)
的单调减区间是(1,2)
⑴求 的解析式;
的解析式;
⑵若对任意的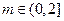 ,关于
,关于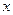 的不等式
的不等式 在
在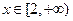 时有解,求实数
时有解,求实数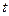 的取值范围.
的取值范围.
(本小题满分12分)
椭圆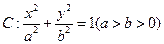 的离心率
的离心率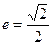 ,过右焦点
,过右焦点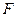
 的直线
的直线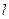 与椭圆
与椭圆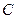 相交
相交
于A、B两点,当直线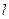 的斜率为1时,坐标原点
的斜率为1时,坐标原点 到直线
到直线 的距离为
的距离为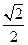
⑴求椭圆C的方程;
⑵椭圆C上是否存在点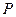 ,使得当直线
,使得当直线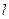 绕点
绕点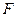 转到某一位置时,有
转到某一位置时,有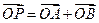 成
成
立?若存在,求出所有满足条件的点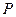 的坐标及对应的直线方程;若不存在,请说明理由.
的坐标及对应的直线方程;若不存在,请说明理由.
(本小题满分12分)
某商品进货价每件50元,据市场调查,当销售价格(每件x元)为50<x≤80时,每
天售出的件数为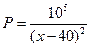 ,若要使每天获得的
,若要使每天获得的 利润最多,销售价格每件应定为多少元
利润最多,销售价格每件应定为多少元 ?
?
(本小题满分12分)
如图,矩形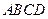 中,
中,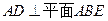 ,
,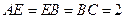 ,
, 为
为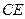 上的点,且
上的点,且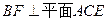 ,
,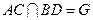 .
.
(Ⅰ)求证: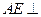 平面
平面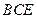 ;
;
(Ⅱ)求证: 平面
平面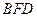 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.