徐州、苏州两地相距500千米,一辆货车从徐州匀速行驶到苏州,规定速度不得超过100千米/小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为0.01;固定部分为a元(a>0)
(1)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;(2)为了使全程运输成本最小,汽车应以多大速度行驶?
【原创】(本小题满分12分)某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表1所示
表1
| 参加社团活动 |
不参加社团活动 |
合计 |
|
| 学习积极性高 |
17 |
8 |
25 |
| 学习积极性一般 |
5 |
20 |
25 |
| 合计 |
22 |
28 |
50 |
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
 |
0.05 |
0.01 |
0.001 |
 |
3.841 |
6.635 |
10.828 |

【改编】(本小题满分12分)已知函数 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当 时,求函数
时,求函数 的值域.
的值域.
【原创】(本小题满分13分)已知函数 ,其中
,其中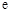 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若对任意 ,不等式
,不等式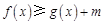 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)试探究当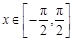 时,方程
时,方程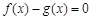 解的个数,并说明理由.
解的个数,并说明理由.
(本小题满分13分)如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: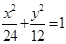 ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆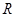 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
,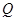 .
.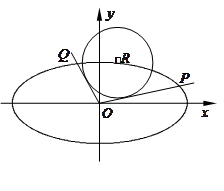
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆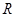 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为 ,
,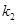 ,求证:
,求证: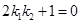 ;
;
(3)试问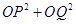 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
(本小题满分12分)已知数列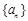 是递增的等差数列,
是递增的等差数列,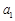 ,
, 是方程
是方程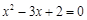 的两根.
的两根.
(Ⅰ)求数列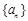 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前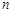 项和
项和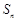 .
.