玉树地震发生后,某地震救援队探测出某建筑废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3米,探测线与地面的夹角分别是30°和60°,如图所示,试确定点C的深度.(结果精确到0.1米,参考数据: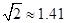 ,
, )
)
(2014年辽宁鞍山12分)如图,在直角△ABD中,∠ADB=90°,∠ABD=45°,点F为直线AD上任意一点,过点 A 作直线AC⊥BF,垂足为点E,直线AC交直线BD于点C. 过点F作FG∥BD,交直线AB于点G.
(1)如图1,点F在边 AD上,则线段FG,DC,BD之间满足的数量关系是 ;
(2)如图 2,若点F在边AD 的延长线上,则线段FG,DC,BD 之间满足的数量关系是 . 证明你的结论;
(3)如图3,在(2)的条件下,若DF=6,GF=10,将一个 45°角的顶点与点B 重合,并绕点B旋转,这个角的两边分别交线段FG 于M,N两点,当FM=2时,求线段NG 的长.
(2014年江西抚州10分)【试题背景】
已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.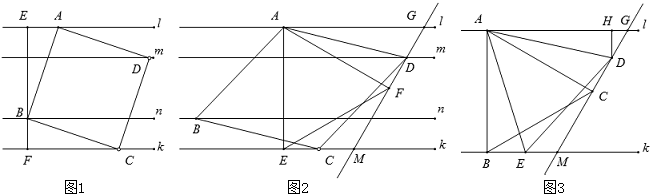
【探究1】
(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F,求正方形ABCD的边长.
【探究2】
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,则矩形ABCD的宽为 .(直接写出结果即可)
【探究3】
如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l、k于点G、点M.求证:EC=DF.
【拓展】
(4)如图3,l∥k,等边△ABC的顶点A、B分别落在直线l、k上,AB⊥k于点B,且AB=4,∠ACD=90°,直线CD分别交直线l、k于点G、点M、点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.
猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.
(年江苏宿迁附加10分)如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
(2014年江苏苏州9分)如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别与l1,l2重合,AB=4 cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
(1)如图①,连接OA,AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围.(解答时可以利用备用图画出相关示意图)
(年江苏南京8分)如图,在Rt△ABC中,∠ACB=90°,AC="4" cm ,BC="3" cm,⊙O为△ABC的内切圆.
(1)求⊙O的半径;
(2)点P从点B沿边BA向点A以点1cm/s 的速度匀速运动,以点P为圆心,PB长为半径作圆. 设点P运动的时间为 t s. 若⊙P与⊙O相切,求t的值.