(2014年江苏苏州9分)如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别与l1,l2重合,AB=4 cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
(1)如图①,连接OA,AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围.(解答时可以利用备用图画出相关示意图)

如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF、FD.
(1)求证:四边形AFDC是平行四边形;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了部分学生进行调查。对数据进行整理,得到下面两个都不完整的扇形统计图(图1)和条形统计图(图2):
(1)该校数学兴趣小组采取的调查方式是 (填“普查”或“抽样调查”);一共调查了名学生;
(2)求扇形统计图中的m,并补全条形统计图;
(3)求扇形统计图中,“乘私家车”所对应扇形的圆心角的度数;
(4)小明说:“为了调查方便,全部在同一个年级抽取.” 这样的抽样是否合理?请说明理由;
(5)根据调查的结果,估计全校2000名学生骑车上学有多少人?
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标(,);
(2)将△ABC的三个顶点的横、纵坐标都乘以-1,分别得到对应点A2、B2、C2,画出△A2B2C2,则△ABC和△A2B2C2关于对称;
(3)将△ABC在网格中平移,使点B的对应点B3坐标为(-6,1),画出△A3B3C3.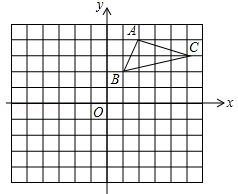
直线l1平行于直线l2,直线l3、l4分别与l1、l2交于点B、F和A、E,点D是直线l3上一动点,DC∥AB交l4于点C.
(1)如图,当点D在l1、l2两线之间运动时,试找出∠BAD、∠DEF、∠ADE之间的关系,并说明理由;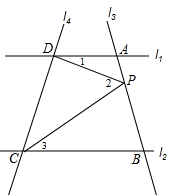
(2)当点D在l1、l2两线外侧运动时,试探究∠BAD、∠DEF、∠ADE之间的关系(点D和B、F不重合),画出图形,给出结论,不必说明理由.
某校为了更好地开展“阳光体育一小时”活动,围绕着“你最喜欢的体育活动项目是什么(只写一项)?”的问题,对本校学生进行了随机抽样调查,以下是根据得到的相关数据绘制的统计图的一部分.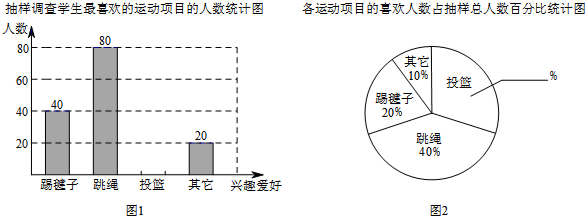
各年级学生人数统计表
| 年级 |
七年级 |
八年级 |
九年级 |
| 学生人数 |
180 |
120 |
请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校七年级学生比九年级学生少20人,请你补全上表,并利用样本数据估计全校学生中最喜欢踢毽子运动的人数约为多少?