（2014年辽宁鞍山12分）如图，在直角△ABD中，∠ADB=90°，∠ABD=45°，点F为直线AD上任意一点，过点 A 作直线AC⊥BF，垂足为点E，直线AC交直线BD于点C. 过点F作FG∥BD，交直线AB于点G.
（1）如图1，点F在边 AD上，则线段FG，DC，BD之间满足的数量关系是 ；
（2）如图 2，若点F在边AD 的延长线上，则线段FG，DC，BD 之间满足的数量关系是 . 证明你的结论；
（3）如图3，在（2）的条件下，若DF=6，GF=10，将一个 45°角的顶点与点B 重合，并绕点B旋转，这个角的两边分别交线段FG 于M，N两点，当FM=2时，求线段NG 的长.
解方程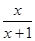
－
＝1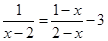
化简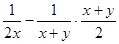
（1+
）÷
．
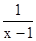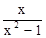解不等式组：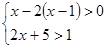
并把解集在数轴上表示出来。
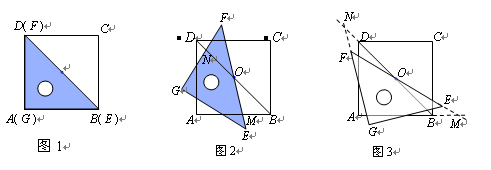
如图1，一等腰直角三角尺GEF（∠EGF=90°,∠GEF=∠GFE=45°,GE=GF）的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．如图2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN相等吗？并说明理由；
若三角尺GEF旋转到如图3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？请说明理由．
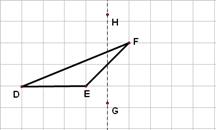
如图，在正方形网格上有一个△DEF。作△DEF关于直线HG的轴对称图形△ABC（不写作法）;
作EF边上的高（不写作法）;
若网格上的最小正方形边长为1，求△DEF的面积.
