如图,我国甲、乙两艘海监执法船某天在某岛附近海域巡航,某一时刻这两艘船分别位于该岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往C处海域巡查的任务,并测得C处位于A处北偏东59°方向,位于B处北偏西44°方向.若甲、乙两船分别沿AC,BC方向航行,且平均速度分别是20海里/时,18海里/时,试估算哪艘船先赶到C处.
(参考数据:cos59°≈0.52,cos44°≈0.72)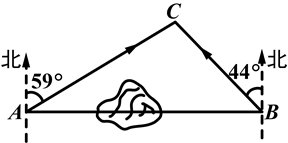
在一次夏令营活动中,小霞同学从营地A点出发,沿北偏东60度方向走了500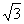 m到达B地,然后再沿北偏西30度方向走了500m到达目的地C.
m到达B地,然后再沿北偏西30度方向走了500m到达目的地C.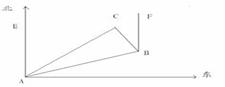
(1)求A,C两地之间的距离.
(2)确定目的地C在营地A的什么方向?
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥CO. 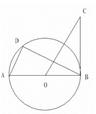
(1)试说明△ADB与△OBC相似.
(2)若AB=2,BC=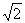 ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
已知关于x的方程x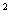 -2(m+1)x+m
-2(m+1)x+m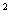 =0.
=0.
(1)当m为何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求出这两个根.
已知:如图,∠ABC,∠ACB的平分线相交于点F,过F作DE∥BC,交AB于D,交AC于E.试探索BD,CE与DE之间的数量关系,并证明你的结论.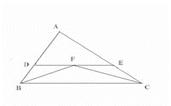
已知一次函数y=kx+k的图象与反比例函数y=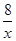 的图像在第二象限交于点B(4,n),(1)求n的值(2)求一次函数的解析式.
的图像在第二象限交于点B(4,n),(1)求n的值(2)求一次函数的解析式.