(本题满分14分)已知函数
 。
。
(Ⅰ)若函数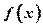 在
在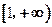 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(Ⅱ)当 时,求
时,求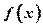 在
在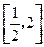 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)当 时,求证:对大于
时,求证:对大于 的任意正整数
的任意正整数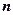 ,都有
,都有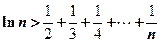 。
。
(本题满分12分)椭圆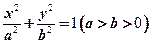 的左、右焦点分别为
的左、右焦点分别为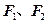 ,过
,过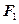 的直线
的直线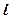 与椭圆交于
与椭圆交于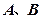 两点。
两点。
(Ⅰ)若点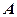 在圆
在圆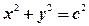 (
(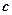 为椭圆的半焦距)上,且
为椭圆的半焦距)上,且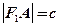 ,求椭圆的离心率;
,求椭圆的离心率; (Ⅱ)若函数
(Ⅱ)若函数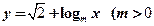 且
且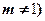 的图象,无论
的图象,无论 为何值时恒过定点
为何值时恒过定点 ,求
,求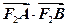 的取值范围。
的取值范围。
(本题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班 位女同学,
位女同学, 位男同学中随机抽取一个容量为
位男同学中随机抽取一个容量为 的样本进行分析。
的样本进行分析。
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(Ⅱ)随机抽取 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: ;
;
物理成绩由低到高依次为: ,若规定
,若规定 分(含
分(含 分)以
分)以 上为优秀,记
上为优秀,记 为这
为这 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若这 位同学的数学、物理分数事实上对应下表:
位同学的数学、物理分数事实上对应下表:
| 学生编号 |
 |
 |
 |
 |
 |
 |
 |
 |
数学分数 |
 |
 |
 |
 |
 |
 |
 |
 |
物理分数 |
 |
 |
 |
 |
 |
 |
 |
 |
根据上表数据可知,变量 与
与
 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出 与
与 的线性回归方程(系数精确到
的线性回归方程(系数精确到 ).(参考公式:
).(参考公式: ,其中
,其中 ,
, ; 参考数据:
; 参考数据: ,
, ,
, ,
, ,
, ,
, ,
, )
)
(本题满分12分)数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, 。
。
(Ⅰ)求
 与
与 的关系式,并求
的关系式,并求 的通项公式;
的通项公式;
(Ⅱ)求和 。
。
已知 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且 。
。
(Ⅰ)若 ,求
,求 的值; (Ⅱ)若
的值; (Ⅱ)若 的面积
的面积 ,求
,求 的值。
的值。