如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=
，直线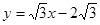
经过点C，交y轴于点G．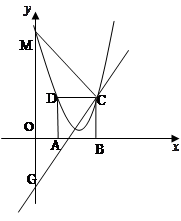
（1）求C，D坐标；
（2）已知抛物线顶点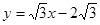上，且经过C，D，若抛物线与y交于点M连接MC，设点Q是线段下方此抛物线上一点，当点Q运动到什么位置时，△MCQ的面积最大？求出此时点Q的坐标和面积的最大值．
（3）将（2）中抛物线沿直线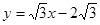平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）。平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？若存在，请求 出此时抛物线的解析式；若不存在，请说明理由．
已知：OA、OB是⊙O的半径，且OA⊥OB，P是射线OA上一点(点A除外)，直线BP交⊙O于点Q，过Q作⊙O的切线交直线OA与点E。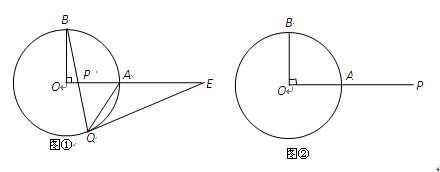
（1）如图①，若点P在线段OA上，求证：∠OBP+∠AQE=45°；(本题4分)
（2）探究：若点P在线段OA的延长线上，其它条件不变，∠OBP与∠AQE之间是否存在某种确定的等量关系？请你完成图②，并写出结论(不需要证明)。(本题3分)
已知三角形ABC中，AB=AC，点A，B，C在以O为圆心的同一个圆上，圆心O到BC的距离为3cm，圆的半径为7cm,求腰长AB.
某服装店出售某品牌的棉衣，平均每天可卖30件，每件盈利50元，为了减少库存迎接“元旦”的到来，商店决定降价销售，增加利润，经调查每件降价5元，则每天可多卖10件，现要想平均每天获利2000元，且让顾客得到实惠，那么每件棉衣应降价多少元？
如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．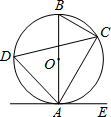
（1）求∠ABC的度数；(本题2分)
（2）求证：AE是⊙O的切线；(本题2分)
（3）当BC=4时，求劣弧AC的长．(本题3分)
某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．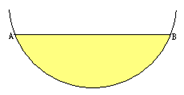
（1）请你用直尺和圆规补全这个输水管道的圆形截面（保留作图痕迹）(本题3分)
（2）若这个输水管道有水部分的水面宽AB＝16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．(本题4分)