(本小题满分12分)已知点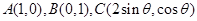
(1)若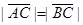 ,求
,求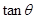 的值;
的值;
(2)若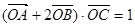 ,其中
,其中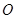 为坐标原点,求
为坐标原点,求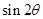 的值。
的值。
如图,椭圆的中心在原点,其左焦点 与抛物线
与抛物线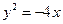 的焦点重合,过
的焦点重合,过 的直线
的直线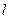 与椭圆交于A、B两点,与抛物线交于C、D两点.当直线
与椭圆交于A、B两点,与抛物线交于C、D两点.当直线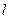 与x轴垂直时,
与x轴垂直时,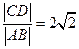 .
.
(Ⅰ)求椭圆的方程;
(II)求过点O、 ,并且与椭圆的左准线相切的圆的方程;
,并且与椭圆的左准线相切的圆的方程;
(Ⅲ)求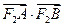 的最大值和最小值.
的最大值和最小值.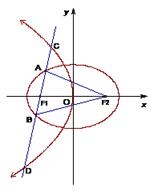
已知点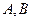 分别是射线
分别是射线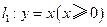 ,
,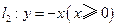 上的动点,
上的动点,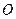 为坐标原点,且
为坐标原点,且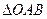 的面积为定值2.
的面积为定值2.
(I)求线段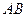 中点
中点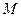 的轨迹
的轨迹 的方程;
的方程;
(II)过点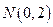 作直线
作直线 ,与曲线
,与曲线 交于不同的两点
交于不同的两点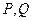 ,与射线
,与射线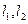 分别交于点
分别交于点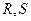 ,若点
,若点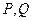 恰为线段
恰为线段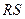 的两个三等分点,求此时直线
的两个三等分点,求此时直线 的方程.
的方程.
已知双曲线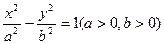 的一条渐近线方程为
的一条渐近线方程为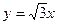 ,两条准线的距离为l.
,两条准线的距离为l.
(1)求双曲线的方程;
(2)直线l过坐标原点O且和双曲线交于两点M、N,点P为双曲线上异于M、N的一点,且直线PM,PN的斜率均存在,求kPM·kPN的值.
已知定圆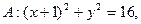 圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
(I)求曲线C的方程;
(II)若点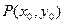 为曲线C上一点,求证:直线
为曲线C上一点,求证:直线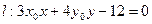 与曲线C有且只有一个交点.
与曲线C有且只有一个交点.
已知抛物线 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(I)求抛物线C的焦点坐标;
(II)若点M满足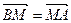 ,求点M的轨迹方程.
,求点M的轨迹方程.