（本小题6分）图中折线表示芳芳骑自行车离家的距离与时间的关系，她9点离开家，15点回家，请根据图象回答下列问题：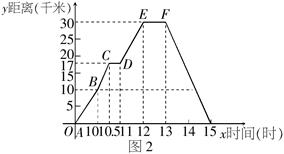
（1）芳芳到达离家最远的地方时，离家________千米；
（2）第一次休息时离家________ 千米；
（3）她在10：00~10：30的平均速度是_________；
（4）芳芳一共休息了_________ 小时；
（5）芳芳返回用了____________小时；
（6）返回时的平均速度是__________．
某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本=每件的成本×每天的销售量）
如图，AB是⊙O的直径，点F，C是⊙O上两点，且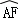
=
=
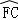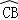，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．
（1）求证：CD是⊙O的切线；
（2）若CD=2
，求⊙O的半径．
在一幅长8分米，宽6分米的矩形风景画的四周镶上宽度相同的金色纸边，制成一幅矩形挂图．如果要使整个挂图的面积是80平方分米，求金色纸边的宽．
如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A，B，C都在格点上，将△ABC绕点A顺时针方向旋转90°得到△AB′C′
（1）在正方形网格中，画出△AB′C′；
（2）计算线段AB在变换到AB′的过程中扫过区域的面积．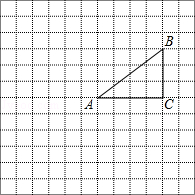
用适当的方法解方程:
（1）x2－2x－1＝0（2）3x（x+2）=5（x+2）