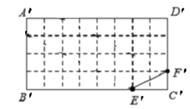
（本小题5分）我们定义：如图1，矩形MNPQ中，点K、O、G、H分别在NP、PQ、QM、MN上，若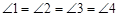
，则称四边形KOGH为矩形MNPQ的反射四边形．如图2、图3四边形ABCD、A’B’C’D’均为矩形，它们都是由32个边长为1的正方形组成的图形，点E、F、E’、F’分别在BC、CD、B’C’、C’D’边上，试利用正方形网格在图2、图3中分别画出矩形ABCD和矩形A’B’C’D’的反射四边形EFGH和E’F’G’H’．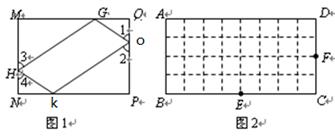
已知抛物线
用配方法求出它的顶点坐标、对称轴.
．抛物线
与
轴交于A,B两点，与
轴交于C点，且A(
,0)。
（1）求抛物线的解析式及顶点坐标D的坐标；
（2）判断
的形状，证明你的结论；（3）点M（m,0）是
轴上的一个动点，当MC+MD的值最小时，求m的值。
．某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）
（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？
（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？
如图，已知梯形ABCD中，AB//CD，AB="2,CD=5," ∠ABC=90°,E是BC上一点，若把△CDE沿折痕折过去，C点恰好与A重合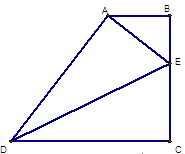
求：（1）BC的长
（2）tan∠CDE的值
抛物线y =" –" x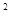
+ (m – 1 )x + m与y轴交于( 0，3 ）点
．
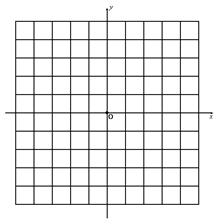
(1) 求出m的值并画出这条抛物线；
(2) 求它与 x 轴的交点和抛物线顶点的坐标； .
(3) x取什么值时，抛物线在x轴上方？
(4) x取什么值时，y的值随 x值的增大而减小？