（本题3+3+4+4分）如图，在平面直角坐标系中，抛物线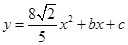
经过点A（
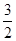，0）和点B（1，
），与x轴的另一个交点为C，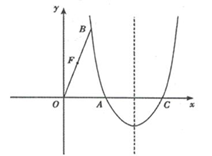
（1）求抛物线的表达式；（2）点D在对称轴的右侧，x轴上方的抛物线上，且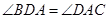
，求点D的坐标；
（3）在（2）的条件下，连接BD，交抛物线对称轴于点E，连接AE
①判断四边形OAEB的形状，并说明理由；
②点F是OB的中点，点M是直线BD上的一个动点，且点M与点B不重合，当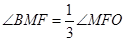
，请直接写出线段BM的长。
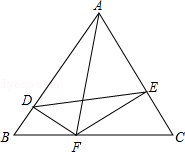
如图，在三角形纸片ABC中，AD平分∠BAC，将△ABC折叠，使点A与点D重合，展开后折痕分别交AB、AC于点E、F，连接DE、DF．求证：四边形AEDF是菱形．
解方程组：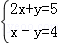
．
计算：
（1）32﹣|﹣2|﹣（π﹣3）0+
；
（2）（1+
）÷
．
已知二次函数y=﹣x2+bx+c的对称轴为x=2，且经过原点，直线AC解析式为y=kx+4，
（1）求二次函数解析式；
（2）若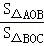
=
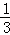，求k；
（3）若以BC为直径的圆经过原点，求k．
△ABC为等边三角形，边长为a，DF⊥AB，EF⊥AC，
（1）求证：△BDF∽△CEF；
（2）若a=4，设BF=m，四边形ADFE面积为S，求出S与m之间的函数关系，并探究当m为何值时S取最大值；
（3）已知A、D、F、E四点共圆，已知tan∠EDF=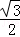
，求此圆直径．