“校园手机”现象越来越受到社会的关注.某校小记者随机调查了某地区若干名学生和家长对学生带手机现象的看法,统计整理并制作了如下的统计图: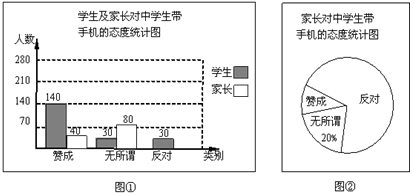
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的家长大约有多少名?
已知函数 图像上的点
图像上的点 处的切线方程为
处的切线方程为 .
.
(1)若函数 在
在 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)函数 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
一台机器使用的时候较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速χ(转/秒) |
16 |
14 |
12 |
8 |
| 每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
(1)画出散点图,并通过散点图确定变量y对χ是否线性相关;
(2)如果y对χ有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
参考公式:线性回归方程的系数公式:
2010年上海世博会举办时间为2010年5月1日--10月31日.此次世博会福建馆招募了60名志愿者,某高校有13人入选,其中5人为中英文讲解员,8人为迎宾礼仪,它们来自该校的5所学院(这5所学院编号为1、2、3、4、5号),人员分布如图所示. 若从这13名入选者中随机抽出3人.
(1)求这3人所在学院的编号正好成等比数列的概率;
(2)求这3人中中英文讲解员人数的分布列及数学期望.
已知 展开式中的倒数第三项的系数为45,求:
展开式中的倒数第三项的系数为45,求:
(1)含 的项;
的项;
(2)系数最大的项.
(本小题满分12分)已知函数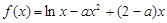 .
.
(1)讨论 的单调性;
的单调性;
(2)设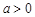 ,证明:当
,证明:当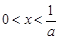 时,
时, ;
;
(3)若函数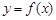 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
证明: (x0)<0.
(x0)<0.